题目内容
 如图,AB=CD,DE⊥AC,BF⊥AC,垂足分别为E、F,要使△ABF≌△CDE,需添加个条件,可以是( )
如图,AB=CD,DE⊥AC,BF⊥AC,垂足分别为E、F,要使△ABF≌△CDE,需添加个条件,可以是( )①∠B=∠D ②DE=BF ③AE=CF ④AB∥CD.
| A、① | B、①或② |
| C、①或②或④ | D、四个条件中的任意一个 |
考点:全等三角形的判定
专题:
分析:本题要判定△ABF≌△CDE,已知AB=CD,∠BFA=∠DEC=90°,具备了一边一角对应相等,故添加①∠B=∠D ②DE=BF ③AE=CF ④AB∥CD后可分别根据AAS、HL、HL、AAS能判定△ABF≌△CDE.
解答:解:在△ABF与△CDE中,AB=CD,
由DE⊥AC,BF⊥AC,可得∠BFA=∠DEC=90°.
①添加∠B=∠D后,满足AAS,符合题意;
②添加DE=BF后,满足HL,符合题意;
③添加AE=DF,即AF=CE后,满足HL,符合题意;
④添加AB∥CD,即∠A=∠C后,满足AAS,符合题意.
故选D.
由DE⊥AC,BF⊥AC,可得∠BFA=∠DEC=90°.
①添加∠B=∠D后,满足AAS,符合题意;
②添加DE=BF后,满足HL,符合题意;
③添加AE=DF,即AF=CE后,满足HL,符合题意;
④添加AB∥CD,即∠A=∠C后,满足AAS,符合题意.
故选D.
点评:本题考查了全等三角形的判定定理的应用,注意:判定两直角三角形全等的判定定理有SAS,ASA,AAS,SSS,HL.

练习册系列答案
相关题目
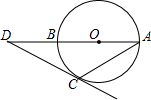 如图,AB是⊙O的直径,DC切⊙O于C,若∠A=25°,则∠D等于( )
如图,AB是⊙O的直径,DC切⊙O于C,若∠A=25°,则∠D等于( )| A、40° | B、50° |
| C、60° | D、70° |
若关于x的方程
=1-
有增根,则k的值为( )
| 3 |
| x-1 |
| k |
| 1-x |
| A、3 | B、1 | C、0 | D、-1 |
 如图,一次函数y=-2x+12分别与x轴、y轴交于点A、B,点C是线段AB的中点,点D在线段OC上,且OD=2CD.
如图,一次函数y=-2x+12分别与x轴、y轴交于点A、B,点C是线段AB的中点,点D在线段OC上,且OD=2CD.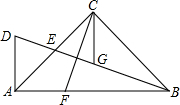 如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,过点A作AD⊥AB交BE的延长线于点D,CG平分∠ACB交BD于点G,F为AB边上一点,连接CF,且∠ACF=∠CBG.求证:
如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,过点A作AD⊥AB交BE的延长线于点D,CG平分∠ACB交BD于点G,F为AB边上一点,连接CF,且∠ACF=∠CBG.求证: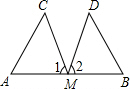 已知:如图,M是AB的中点,∠1=∠2,MC=MD.求证:△ACM≌△BDM.
已知:如图,M是AB的中点,∠1=∠2,MC=MD.求证:△ACM≌△BDM.