题目内容
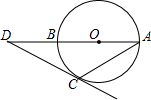如图，AB是⊙O的直径，DC切⊙O于C，若∠A=25°，则∠D等于（ ）| A、40° | B、50° |
| C、60° | D、70° |
考点：切线的性质
专题：
分析：先连接BC，由于AB 是直径，可知∠BCA=90°，而∠A=25°，易求∠CBA，又DC是切线，利用弦切角定理可知∠DCB=∠A=25°，再利用三角形外角性质可求∠D．
解答：
解：连接BC，
∵AB 是直径，
∴∠BCA=90°，
又∵∠A=25°，
∴∠CBA=90°-25°=65°，
∵DC是切线，
∴∠BCD=∠A=25°，
∴∠D=∠CBA-∠BCD=65°-25°=40°．
故选A．
解：连接BC，∵AB 是直径，
∴∠BCA=90°，
又∵∠A=25°，
∴∠CBA=90°-25°=65°，
∵DC是切线，
∴∠BCD=∠A=25°，
∴∠D=∠CBA-∠BCD=65°-25°=40°．
故选A．
点评：本题考查了直径所对的圆周角等于90°、弦切角定理、三角形外角性质．解题的关键是连接BC，构造直角三角形ABC．
练习册系列答案
中考解读考点精练系列答案
相关题目
如图，已知△ABC中，BD平分∠ABC，CE=CD，DB=DE，∠E=30°．
如图，AB=CD，DE⊥AC，BF⊥AC，垂足分别为E、F，要使△ABF≌△CDE，需添加个条件，可以是（ ）①∠B=∠D ②DE=BF ③AE=CF ④AB∥CD．
| A、① | B、①或② |
| C、①或②或④ | D、四个条件中的任意一个 |
计算
÷
÷
的结果是（ ）
1
|
2
|
1
|
A、
| ||||
B、
| ||||
C、
| ||||
D、
|