题目内容
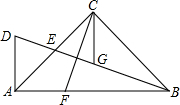 如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,过点A作AD⊥AB交BE的延长线于点D,CG平分∠ACB交BD于点G,F为AB边上一点,连接CF,且∠ACF=∠CBG.求证:
如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,过点A作AD⊥AB交BE的延长线于点D,CG平分∠ACB交BD于点G,F为AB边上一点,连接CF,且∠ACF=∠CBG.求证:(1)BG=CF;
(2)DG=CF.
考点:全等三角形的判定与性质,线段垂直平分线的性质
专题:证明题
分析:(1)首先证出∠CAF=∠BCG,得到△BCG≌△CAF,由三角形性质得出BG=CF;
(2)连接AG,证明△ACG≌△BCG,得出AG=BG,再证出∠D=∠GAD,得出AG=DG,从而证出DG=CF.
(2)连接AG,证明△ACG≌△BCG,得出AG=BG,再证出∠D=∠GAD,得出AG=DG,从而证出DG=CF.
解答:证明:(1)∵∠ACB=90°,AC=BC,CG平分∠ACB,
∴∠CAF=∠CBA=45°,∠BCG=∠ACG=45°,
∴∠BCG=∠CAF=45°
 ∵∠CBG=∠ACF,AC=BC
∵∠CBG=∠ACF,AC=BC
∴△BCG≌△CAF,
∴BG=CF;
(2)连接AG,如图所示:
∵AC=BC,∠ACG=∠BCG,CG=CG,
∴△ACG≌△BCG,
∴AG=BG,
∴∠GBA=∠GAB,
∵AD⊥AB
∴∠D=90°-∠GBA=90°-∠GAB=∠GAD,
∴AG=DG.
∵由(1)BG=CF,
∴DG=CF.
∴∠CAF=∠CBA=45°,∠BCG=∠ACG=45°,
∴∠BCG=∠CAF=45°
 ∵∠CBG=∠ACF,AC=BC
∵∠CBG=∠ACF,AC=BC∴△BCG≌△CAF,
∴BG=CF;
(2)连接AG,如图所示:
∵AC=BC,∠ACG=∠BCG,CG=CG,
∴△ACG≌△BCG,
∴AG=BG,
∴∠GBA=∠GAB,
∵AD⊥AB
∴∠D=90°-∠GBA=90°-∠GAB=∠GAD,
∴AG=DG.
∵由(1)BG=CF,
∴DG=CF.
点评:本题考查了全等三角形的判定与性质和等腰三角形的判定与性质;证明三角形全等是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
当k•b<0时,一次函数y=kx-b的图象大致是( )
A、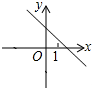 |
B、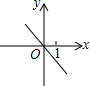 |
C、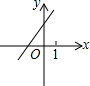 |
D、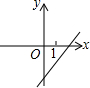 |
 如图,AB=CD,DE⊥AC,BF⊥AC,垂足分别为E、F,要使△ABF≌△CDE,需添加个条件,可以是( )
如图,AB=CD,DE⊥AC,BF⊥AC,垂足分别为E、F,要使△ABF≌△CDE,需添加个条件,可以是( )①∠B=∠D ②DE=BF ③AE=CF ④AB∥CD.
| A、① | B、①或② |
| C、①或②或④ | D、四个条件中的任意一个 |
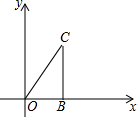 如图,已知△OBC是直角三角形,点B在x轴的正半轴上,∠OBC=90°,且OB=1,BC=1.5,以原点O为位似中心,将线段BC扩大为原来的两倍,则在第一象限内点C经过变换后的坐标为( )
如图,已知△OBC是直角三角形,点B在x轴的正半轴上,∠OBC=90°,且OB=1,BC=1.5,以原点O为位似中心,将线段BC扩大为原来的两倍,则在第一象限内点C经过变换后的坐标为( )| A、(1,3) |
| B、(2,1.5) |
| C、(2,3) |
| D、(3,2) |
