题目内容
 如图所示,△ABC中,若点O是∠B、∠C的角平分线的交点,且∠ABC=50°,∠ACB=60°,则∠OAB=
如图所示,△ABC中,若点O是∠B、∠C的角平分线的交点,且∠ABC=50°,∠ACB=60°,则∠OAB=考点:三角形内角和定理
专题:
分析:先根据三角形内角和定理求出∠BAC的度数,再根据角平分线性质即可得出结论.
解答:解:∵△ABC中,∠ABC=50°,∠ACB=60°,
∴∠BAC=180°-50°-60°=70°.
∵点O是∠B、∠C的角平分线的交点,
∴OA是∠BAC的平分线,
∴∠OAB=
∠BAC=
×70°=35°.
故答案为:35°.
∴∠BAC=180°-50°-60°=70°.
∵点O是∠B、∠C的角平分线的交点,
∴OA是∠BAC的平分线,
∴∠OAB=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:35°.
点评:本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
相关题目
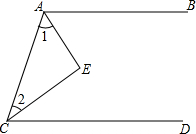 如图,AE、CE分别平分∠BAC和∠ACD,∠1和∠2互余,试说明AB∥CD.
如图,AE、CE分别平分∠BAC和∠ACD,∠1和∠2互余,试说明AB∥CD.