题目内容
12.先化简,再求值:(m-n)(m+n)+(m+n)2-2m2,其中m、n满足方程组$\left\{\begin{array}{l}m+2n=1\\ 3m-2n=11\end{array}\right.$.分析 原式利用平方差公式、完全平方公式化简,去括号合并得到最简结果,求出方程组的解得到m与n的值,代入计算即可求出值.
解答 解:$\left\{\begin{array}{l}{m+2n=1①}\\{3m-2n=11②}\end{array}\right.$,
①+②,得4m=12,解得:m=3,
将m=3代入①,得9-2n=11,解得n=-1,
故方程组的解是$\left\{\begin{array}{l}m=3\\ n=-1\end{array}\right.$,
(m-n)(m+n)+(m+n)2-2m2=m2-n2+m2+2mn+n2-2m2=2mn,
当m=3,n=-1时,原式=2×3×(-1)=-6.
点评 此题考查了整式的混合运算-化简求值,以及解二元一次方程组,熟练掌握运算法则是解本题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
2.联合国经济和社会事务部于2015年7月29日发布《世界人口展望报告》称,全球人口到2100年将达到112亿(即11 200 000 000人,11 200 000 000这个数据用科学记数法表示为( )
| A. | 11.2×109 | B. | 1.12×1010 | C. | 0.112×1011 | D. | 1.12×1011 |
3.不等式x-1≥1的解集在数轴上表示为( )
| A. |  | B. |  | C. |  | D. |  |
7.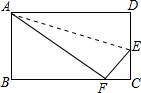 如图,折叠矩形纸片ABCD的一边AD,使点D落在BC边上的点F处,若AB=8,BC=10,则△CEF的周长为( )
如图,折叠矩形纸片ABCD的一边AD,使点D落在BC边上的点F处,若AB=8,BC=10,则△CEF的周长为( )
 如图,折叠矩形纸片ABCD的一边AD,使点D落在BC边上的点F处,若AB=8,BC=10,则△CEF的周长为( )
如图,折叠矩形纸片ABCD的一边AD,使点D落在BC边上的点F处,若AB=8,BC=10,则△CEF的周长为( )| A. | 12 | B. | 16 | C. | 18 | D. | 24 |
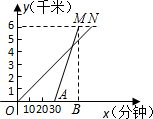 清明小长假期间,小明和小亮相约从学校出发,去距学校6千米的三国古城遗址公园游玩,小明步行但小亮骑自行车,在去公园的全过程中,骑自行车的小亮同学比步行的小明同学少用40分钟,已知骑自行车的速度是步行速度的3倍.
清明小长假期间,小明和小亮相约从学校出发,去距学校6千米的三国古城遗址公园游玩,小明步行但小亮骑自行车,在去公园的全过程中,骑自行车的小亮同学比步行的小明同学少用40分钟,已知骑自行车的速度是步行速度的3倍. 推理填空:
推理填空: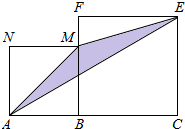 如图,线段AC=n+1(其中n为正整数),点B在线段AC上,在线段AC同侧作正方形ABMN及正方形BCEF,连接AM、ME、EA得到△AME.当AB=1时,△AME的面积记为S1;当AB=2时,△AME的面积记为S2;当AB=3时,△AME的面积记为
如图,线段AC=n+1(其中n为正整数),点B在线段AC上,在线段AC同侧作正方形ABMN及正方形BCEF,连接AM、ME、EA得到△AME.当AB=1时,△AME的面积记为S1;当AB=2时,△AME的面积记为S2;当AB=3时,△AME的面积记为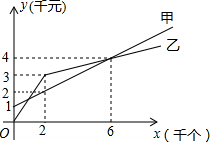 某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分先收取固定的制版费,再按印刷数量收取印刷费,乙厂直接按印刷数量收取印刷费.甲厂的总费用y1(干元)、乙厂的总费用y2(千元)与印制证书数量x(千个)的函数关系图分别如图中甲、乙所示.
某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分先收取固定的制版费,再按印刷数量收取印刷费,乙厂直接按印刷数量收取印刷费.甲厂的总费用y1(干元)、乙厂的总费用y2(千元)与印制证书数量x(千个)的函数关系图分别如图中甲、乙所示. 已知线段AB、BC,∠ABC=90°,求作矩形ABCD.
已知线段AB、BC,∠ABC=90°,求作矩形ABCD.