题目内容
1.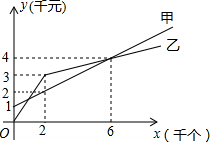 某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分先收取固定的制版费,再按印刷数量收取印刷费,乙厂直接按印刷数量收取印刷费.甲厂的总费用y1(干元)、乙厂的总费用y2(千元)与印制证书数量x(千个)的函数关系图分别如图中甲、乙所示.
某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分先收取固定的制版费,再按印刷数量收取印刷费,乙厂直接按印刷数量收取印刷费.甲厂的总费用y1(干元)、乙厂的总费用y2(千元)与印制证书数量x(千个)的函数关系图分别如图中甲、乙所示.(l)甲厂的制版费为1千元,印刷费为平均每个0.5元,甲厂的费用yl与证书数量x之间的函数关系式为yl=0.5x+1;
(2)当印制证书数量不超过2千个时,乙厂的印刷费为平均每个1.5 元;当印制证书数量超过2千个时,求乙厂的总费用y2与证书数量x之间的函数关系式为y2=$\frac{1}{4}x+\frac{5}{2}$;
(3)若甲厂的总费用高于乙厂,但相差不超过500元,该单位需印制证书数量的范围是6<x≤8或0.5≤x<1.
分析 (1)结合图象便可看出y是关于x的一次函数,从图中可以观察出甲厂的制版费为1千元,一次函数的斜率为0.5,即为证书的单价;
(2)用2到6千个时的费用除以证件个数计算即可得解,设函数解析式后用待定系数法解答即可;
(3)分别求出甲乙两厂的费用y关于证书个数x的函数,根据题意列不等式即可得到结论.
解答 解:(1)制版费1千元,yl=0.5x+1,证书单价0.5元;
故答案为:1;0.5;yl=0.5x+1;
(2)当印制证书数量不超过2千个时,乙厂的印刷费为平均每个=3÷2=1.5元,
故答案为:1.5;
设y2=kx+b,
由图可知,当x=6时,y2=y1=0.5×6+1=4,
所以函数图象经过点(2,3)和(6,4),
所以把(2,3)和(6,4)代入y2=kx+b,
得$\left\{\begin{array}{l}{2k+b=3}\\{6k+b=4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{1}{4}}\\{b=\frac{5}{2}}\end{array}\right.$,所以y2与x之间的函数关系式为y2=$\frac{1}{4}x+\frac{5}{2}$;
故答案为:y2=$\frac{1}{4}x+\frac{5}{2}$;
(3)0<0.5x+1-($\frac{1}{4}x+\frac{5}{2}$)≤0.5,
解得6<x≤8.
当0.5≤x<1时,甲厂的总费用高于乙厂,
故答案为:6<x≤8或0.5≤x<1.
点评 本题主要考查了一次函数和一元一次不等式的实际应用,是各地中考的热点,同学们在平时练习时要加强训练,属于中档题.

练习册系列答案
相关题目
11. 如图,AB为⊙O的直径,四边形ABCD为⊙O的内接四边形,点P在BA的延长线上,PD与⊙O相切,D为切点,若∠BCD=120°,则∠APD的大小为( )
如图,AB为⊙O的直径,四边形ABCD为⊙O的内接四边形,点P在BA的延长线上,PD与⊙O相切,D为切点,若∠BCD=120°,则∠APD的大小为( )
 如图,AB为⊙O的直径,四边形ABCD为⊙O的内接四边形,点P在BA的延长线上,PD与⊙O相切,D为切点,若∠BCD=120°,则∠APD的大小为( )
如图,AB为⊙O的直径,四边形ABCD为⊙O的内接四边形,点P在BA的延长线上,PD与⊙O相切,D为切点,若∠BCD=120°,则∠APD的大小为( )| A. | 45° | B. | 40° | C. | 35° | D. | 30° |
6.方程x2-ax+4=0的两根相等,则a=( )
| A. | 2 | B. | ±4 | C. | -4 | D. | 4 |
10.为了了解某校八年级1000名学生的身高,从中抽取了50名学生并对他们的身高进行统计分析,以下说法正确的是( )
| A. | 1 000名学生是总体 | |
| B. | 抽取的50名学生是样本容量 | |
| C. | 每位学生的身高是个体 | |
| D. | 被抽取的50名学生是总体的一个样本 |
 如图,菱形ABCD的周长为16,∠B=60°,则以AC为边长的正方形ACEF的周长为16.
如图,菱形ABCD的周长为16,∠B=60°,则以AC为边长的正方形ACEF的周长为16.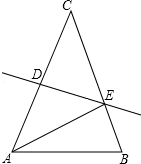 如图,在三角形纸片△ABC中,AC=BC,∠B=70°,将△ABC沿线段DE所在直线对折,使点A、点C重合,连接AE,则∠AED的度数是50度.
如图,在三角形纸片△ABC中,AC=BC,∠B=70°,将△ABC沿线段DE所在直线对折,使点A、点C重合,连接AE,则∠AED的度数是50度.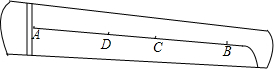 如图,乐器上的一根弦AB=80cm,两个端点A、B固定在乐器板面上,支撑点C是靠近点B的黄金分割点,支撑点D是靠近点A的黄金分割点,求C、D之间的距离.
如图,乐器上的一根弦AB=80cm,两个端点A、B固定在乐器板面上,支撑点C是靠近点B的黄金分割点,支撑点D是靠近点A的黄金分割点,求C、D之间的距离.


