题目内容
7.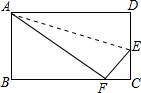 如图,折叠矩形纸片ABCD的一边AD,使点D落在BC边上的点F处,若AB=8,BC=10,则△CEF的周长为( )
如图,折叠矩形纸片ABCD的一边AD,使点D落在BC边上的点F处,若AB=8,BC=10,则△CEF的周长为( )| A. | 12 | B. | 16 | C. | 18 | D. | 24 |
分析 先根据矩形的性质得AD=BC=10,AB=CD=8,再根据折叠的性质得AF=AD=10,EF=DE,在Rt△ABF中,利用勾股定理计算出BF=6,则CF=BC-BF=4,易得△CEF的周长.
解答 解:∵四边形ABCD为矩形,
∴AD=BC=10,AB=CD=8,
∵矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上的F处,
∴AF=AD=10,EF=DE,
在Rt△ABF中,
∵BF=$\sqrt{{AF}^{2}{-AB}^{2}}$=6,
∴CF=BC-BF=10-6=4,
∴△CEF的周长为:CE+EF+CF=CE+DE+CF=CD+CF=8+4=12.
故选A.
点评 本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了矩形的性质和勾股定理,利用勾股定理得CF的长是解答此题的关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
18.不等式x+5≥1的解集在数轴上表示正确的是( )
| A. |  | B. |  | C. |  | D. |  |
17.2016年扬州体育中考现场考试内容有两项,50米跑为必考项目,另在立定跳远、坐位体前屈、实心球和一分钟跳绳中选一项测试.王老师对参加体育中考的九(1)班40名学生的一项选测科目作了统计,列出如图所示的统计表,则本班参加坐位体前屈的人数是14人.
| 组别 | 立定跳远 | 坐位体前屈 | 实心球 | 一分钟跳绳 |
| 频率 | 0.4 | 0.35 | 0.1 | 0.15 |
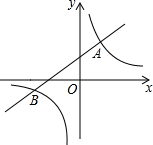 如图,一次函数y=kx+b与反比例函数$y=\frac{m}{x}$的图象相交于A(2,3),B(-3,n)两点.
如图,一次函数y=kx+b与反比例函数$y=\frac{m}{x}$的图象相交于A(2,3),B(-3,n)两点.
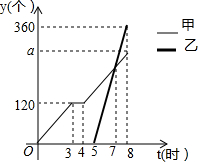 某天,甲组工人加工零件,工作中有一次停产检修机器,然后继续加工.由于任务紧急,乙组工人加入,与甲组工人一起生产零件.两组各自加工零件的数量y(个)与甲组工人加工时间t(时)之间的函数图象如图所示.
某天,甲组工人加工零件,工作中有一次停产检修机器,然后继续加工.由于任务紧急,乙组工人加入,与甲组工人一起生产零件.两组各自加工零件的数量y(个)与甲组工人加工时间t(时)之间的函数图象如图所示.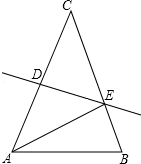 如图,在三角形纸片△ABC中,AC=BC,∠B=70°,将△ABC沿线段DE所在直线对折,使点A、点C重合,连接AE,则∠AED的度数是50度.
如图,在三角形纸片△ABC中,AC=BC,∠B=70°,将△ABC沿线段DE所在直线对折,使点A、点C重合,连接AE,则∠AED的度数是50度.