题目内容
5. 如图,△ABC的中线BE,CF相交于点G,证明:BG=2GE,CG=2GF.
如图,△ABC的中线BE,CF相交于点G,证明:BG=2GE,CG=2GF.
分析 根据三角形中位线性质得出BC=2EF,EF∥BC,根据相似三角形的判定得出△FEG∽△CBG,根据相似三角形的性质定理得出比例式,即可得出答案.
解答 证明:∵△ABC的中线BE,CF相交于点G,
∴BC=2EF,EF∥BC,
∴△FEG∽△CBG,
∴$\frac{EF}{BC}$=$\frac{EG}{BG}$=$\frac{FG}{CG}$,
∵BC=2EF,
∴BG=2GE,CG=2GF.
点评 本题考查了三角形的中位线性质,相似三角形的性质和判定的应用,能根据定理得出比例式和求出BC=2EF是解此题的关键.

练习册系列答案
相关题目
13.x表示一个两位数,y表示一个三位数,如果把x放在y的左边组成一个五位数,那么这个五位数就可以表示为( )
| A. | xy | B. | x+y | C. | 1 000x+y | D. | 10x+y |
 如图,平面直角坐标系中,已知直线y=x上一点P(1,1),C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B.直线AB与直线y=x交于点A,且BD=2AD,连接CD,直线CD与直线y=x交于点Q.
如图,平面直角坐标系中,已知直线y=x上一点P(1,1),C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B.直线AB与直线y=x交于点A,且BD=2AD,连接CD,直线CD与直线y=x交于点Q.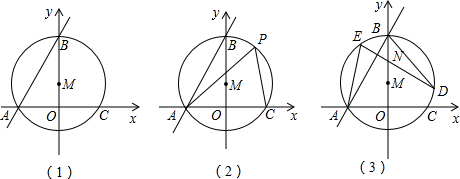
 如图,在平面直角坐标系中,函数y=ax2+bx+c(a>0)的图象的顶点为D点,与y轴交于C点,与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),OB=OC,$\frac{AO}{OC}$=$\frac{1}{3}$.
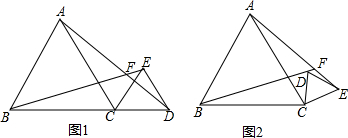
如图,在平面直角坐标系中,函数y=ax2+bx+c(a>0)的图象的顶点为D点,与y轴交于C点,与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),OB=OC,$\frac{AO}{OC}$=$\frac{1}{3}$. 如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:①∠CEG=2∠DCB;②CA平分∠BCG;③∠ADC=∠GCD;④∠DFB=$\frac{1}{2}$∠CGE.
如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:①∠CEG=2∠DCB;②CA平分∠BCG;③∠ADC=∠GCD;④∠DFB=$\frac{1}{2}$∠CGE.