题目内容
14．
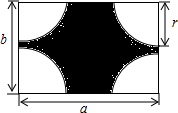如图，有一块长为a米，宽为b米的长方形铁皮，将四个角分别截去半径都是r米的四分之一的圆形．（1）求阴影部分的面积（用含a，b，r的代数式表示）；
（2）当a=8米，b=6米，r=2米时，剩下铁皮的面积是多少平方米？（π取3.14）
分析 （1）阴影部分的面积=长方形铁皮面积-截去半径为r米的圆的面积；
（2）把a=8米，b=6米，r=2米代入（1）中式子即可求出剩余铁皮的面积．
解答 解：（1）由已知得：
剩余铁皮的面积=长方形铁皮面积-截去半径为r米的圆的面积
=ab-πr2（平方米）；
（2）当a=8米，b=6米，r=2米，π取3.14时，
剩余铁皮的面积是：ab-πr2≈8×6-3.14×22=35.44（平方米）．
点评 此题考查的知识点是列代数式及代数式求值，解决问题的关键是读懂题意，找到所求的量的等量关系．要熟练运用长方形面积和圆面积公式．
练习册系列答案
相关题目
如图，在平面直角坐标系中，函数y=ax2+bx+c（a＞0）的图象的顶点为D点，与y轴交于C点，与x轴交于A、B两点，A点在原点的左侧，B点的坐标为（3，0），OB=OC，$\frac{AO}{OC}$=$\frac{1}{3}$．
9．
如图所示，A，B，C三点在正方形网格线的交点处．若将△ACB绕着点A逆时针旋转到如图位置，得到△AC′B′，使A，C，B′三点共线，则旋转角为（ ）
如图所示，A，B，C三点在正方形网格线的交点处．若将△ACB绕着点A逆时针旋转到如图位置，得到△AC′B′，使A，C，B′三点共线，则旋转角为（ ）| A． | 30° | B． | 60° | C． | 20° | D． | 45° |
画出△ABC关于x轴和y轴对称的图形△A1B1C1和△A2B2C2，并指出△A1B1C1和△A2B2C2的顶点坐标．
如图，△ABC的角平分线CD、BE相交于F，∠A=90°，EG∥BC，且CG⊥EG于G，下列结论：①∠CEG=2∠DCB；②CA平分∠BCG；③∠ADC=∠GCD；④∠DFB=$\frac{1}{2}$∠CGE．