题目内容
17.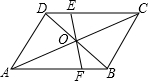 如图,O为?ABCD的对角线的交点,过O点作直线EF分别交CD,AB于点E,F.
如图,O为?ABCD的对角线的交点,过O点作直线EF分别交CD,AB于点E,F.(1)求证:0E=0F;
(2)若AB=5,BC=4,0E=1.5,求四边形EFBC的周长;
(3)若S四CEFB=10,直接写出S?ABCD的值为20.
分析 (1)由四边形ABCD是平行四边形,得到CD∥AB,OD=OB由平行线的性质得到∠CDO=∠ABO,推出△DEO≌△BFO(ASA).根据全等三角形的性质即可得到结论;
(2)根据全等三角形的性质得到OE=OF=1.5,BF=DE,于是得到EF=3,BF+CE=AB=5,即可得到结论;
(3)根据全等三角形的性质即可得到S?ABCD=2S四CEFB=10×2=20.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴CD∥AB,OD=OB
∴∠CDO=∠ABO,
在△DEO与△BFO中,
$\left\{\begin{array}{l}{∠EDO=∠FBO}\\{OD=OB}\\{∠DOE=BOF}\end{array}\right.$
∴△DEO≌△BFO(ASA).
∴OE=OF;
(2)∵△DEO≌△BFO(ASA).
∴OE=OF=1.5,BF=DE,
∴EF=3,BF+CE=AB=5,
∴四边形EFBC的周长=3+5+4=12;
(3)∵△DEO≌△BFO,
同理△CEO≌△AFO,
∵△ADO≌△BCO,
∴S?ABCD=2S四CEFB=10×2=20,
故答案为:20.
点评 此题主要考查了全等三角形的性质与判定、平行四边形的性质,首先利用平行四边形的性质构造全等条件,然后利用全等三角形的性质解决问题.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
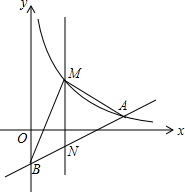 如图,在平面直角坐标系中,已知点A(8,1),B(0,-3),反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A,N是线段AB上一动点(不与A、B重合),MN⊥x轴且与反比例函数的图象交于M点.
如图,在平面直角坐标系中,已知点A(8,1),B(0,-3),反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A,N是线段AB上一动点(不与A、B重合),MN⊥x轴且与反比例函数的图象交于M点.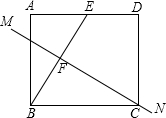 如图,长方形纸片ABCD中,CD=4,点E是AD上的-点,且AE=2,BE的垂直平分线MN恰好过点C,求矩形的一边AD的长度.
如图,长方形纸片ABCD中,CD=4,点E是AD上的-点,且AE=2,BE的垂直平分线MN恰好过点C,求矩形的一边AD的长度.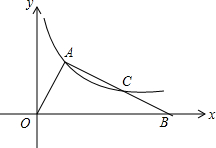 如图,直角△AOB的斜边OB在x轴正半轴上,双曲线y=$\frac{k}{x}$(x>0)经过点A,交AB于点C,且AC=BC,OA=3,则k=3$\sqrt{2}$.
如图,直角△AOB的斜边OB在x轴正半轴上,双曲线y=$\frac{k}{x}$(x>0)经过点A,交AB于点C,且AC=BC,OA=3,则k=3$\sqrt{2}$.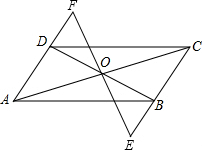 如图,在?ABCD中,对角线AC,BD交于点O,过点O的直线分别交CB,AD的延长线于点E,F,BE与DF相等吗?为什么?
如图,在?ABCD中,对角线AC,BD交于点O,过点O的直线分别交CB,AD的延长线于点E,F,BE与DF相等吗?为什么? 如图,A是函数y=$\frac{k}{x}$上一点.AB⊥x轴于B点,若S△AOB=4.
如图,A是函数y=$\frac{k}{x}$上一点.AB⊥x轴于B点,若S△AOB=4.