题目内容
13.已知二次函数的图象经过原点和(-1,3)且图象与x轴的另一个交点到原点的距离为2,求该二次函数的解析式.分析 根据与x轴的另一交点到原点的距离为2,分这个交点坐标为(-2,0)、(2,0)两种情况,利用待定系数法求函数解析式解答即可.
解答 解:∵图象与x轴的另一个交点到原点的距离为2,
∴这个交点坐标为(-2,0)、(2,0).
∵二次函数的图象经过原点,
∴设二次函数解析式为y=ax2+bx(a≠0),
①当这个交点坐标为(-2,0)时,代入点(-1,3),
$\left\{\begin{array}{l}{a-b=3}\\{4a-2b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-3}\\{b=-6}\end{array}\right.$.
故该二次函数的解析式为y=-3x2-6x;
②当这个交点坐标为(2,0)时,代入点(-1,3),
$\left\{\begin{array}{l}{a-b=3}\\{4a+2b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=1}\\{b=-2}\end{array}\right.$.
故该二次函数的解析式为y=x2-2x.
综上所述,所求的二次函数解析式为:y=-3x2-6x或y=x2-2x.
点评 本题考查了抛物线与x轴的交点,利用待定系数法求二次函数解析式时,注意另一个交点要分两种情况讨论求解,避免漏解而导致出错.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
5. 弹簧的长度y(cm)与所挂物体的质量x(kg)之间的关系是一次函数关系,图象如图所示,则弹簧本身的长度是( )
弹簧的长度y(cm)与所挂物体的质量x(kg)之间的关系是一次函数关系,图象如图所示,则弹簧本身的长度是( )
 弹簧的长度y(cm)与所挂物体的质量x(kg)之间的关系是一次函数关系,图象如图所示,则弹簧本身的长度是( )
弹簧的长度y(cm)与所挂物体的质量x(kg)之间的关系是一次函数关系,图象如图所示,则弹簧本身的长度是( )| A. | 20cm | B. | 12.5cm | C. | 10cm | D. | 9cm |
3.关于x的一元二次方程(a-2)x2+x+a2=0的一个根是0,则a的值为( )
| A. | 2 | B. | -2 | C. | 2或-2 | D. | 0 |
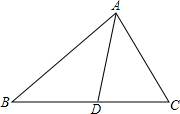 如图所示,AD为△ABC的角平分线,AB=5,AC=4,△ABD和△ABC的面积分别为S△ABD和S△ABC,那么S△ABD:S△ABC=5:9.
如图所示,AD为△ABC的角平分线,AB=5,AC=4,△ABD和△ABC的面积分别为S△ABD和S△ABC,那么S△ABD:S△ABC=5:9.