题目内容
2．已知a，b关于x的一元二次方程1-（x-m）（x-n）=0的两个不想等的实数根，且a＞b，m＜n．则比较a、b、m、n的大小关系为b＜m＜n＜a．分析 可设抛物线解析式为y=（x-m）（x-n），于是得到抛物线与x轴的交点坐标为（m，0），（n，0），再判断当自变量为a、b时二次函数值为1，即y=（x-m）（x-n）=1，然后画出图象，利用图象可得判断a、b、m、n的大小关系．
解答 解：设抛物线解析式为y=（x-m）（x-n），则此抛物线与x轴的交点坐标为（m，0），（n，0），
∵a，b关于x的一元二次方程1-（x-m）（x-n）=0的两个不等的实数根，
∴当自变量为a、b时y=（x-m）（x-n）=1，
即a、b为直线y=1与抛物线y=（x-m）（x-n）两交点的横坐标，
如图：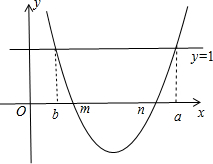
∴b＜m＜n＜a．
故答案为b＜m＜n＜a．
点评 本题考查了抛物线与x轴的交点：从二次函数的交点式y=a（x-x1）（x-x2）（a，b，c是常数，a≠0）可直接得到抛物线与x轴的交点坐标（x1，0），（x2，0）．解决本题的关键是要画出大致图象．
练习册系列答案
相关题目
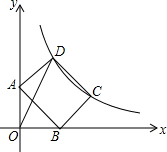如图所示，矩形ABCD的顶点C、D在反比例函数y=$\frac{k}{x}$（k＞0，x＞0）的图象上，顶点A在y轴上，顶点B在x轴上，连接OD，若∠ODC=60°，则$\frac{AB}{AD}$=$\sqrt{3}+1$．
画出函数y=2x+6的图象，利用图象：
