题目内容
4.有一个多边形,它的内角和等于它的外角和的2倍,则它是( )| A. | 三边形 | B. | 四边形 | C. | 五边形 | D. | 六边形 |
分析 n边形的内角和可以表示成(n-2)•180°,外角和为360°,根据题意列方程求解.
解答 解:设多边形的边数为n,依题意,得:
(n-2)•180°=2×360°,
解得n=6.
故选:D.
点评 本题主要考查多边形的内角和计算公式,多边形的外角和.关键是根据题意利用多边形的外角和及内角和之间的关系列出方程求边数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
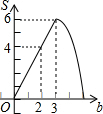
9.如图1,在矩形ABCD中,AB<BC,点E为对角线AC上的一个动点,连接BE,DE,过E作EF⊥BC于F.设AE=x,图1中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是图1中的( )


| A. | 线段BE | B. | 线段EF | C. | 线段CE | D. | 线段DE |
16.如果用总长为120m的篱笆围成一个长方形场地,设长方形的面积为S(m2),周长为C(m),一边长为a(m),那么S,C,a中是变量的是( )
| A. | S和C | B. | S和a | C. | C和a | D. | S,C,a |
14. 在西安市开展的“双城联创”活动中,某校倡议七年级学生利用双休日在各自社区参加义务劳动,为了解同学们劳动情况,学校随机抽查了部分学生的劳动时间,并用得到的数据绘制成不完整的统计图表,如图所示:
在西安市开展的“双城联创”活动中,某校倡议七年级学生利用双休日在各自社区参加义务劳动,为了解同学们劳动情况,学校随机抽查了部分学生的劳动时间,并用得到的数据绘制成不完整的统计图表,如图所示:
(1)统计表中的x=40,y=0.18;补全条形统计图.
(2)求所有被调查同学的平均劳动时间.
 在西安市开展的“双城联创”活动中,某校倡议七年级学生利用双休日在各自社区参加义务劳动,为了解同学们劳动情况,学校随机抽查了部分学生的劳动时间,并用得到的数据绘制成不完整的统计图表,如图所示:
在西安市开展的“双城联创”活动中,某校倡议七年级学生利用双休日在各自社区参加义务劳动,为了解同学们劳动情况,学校随机抽查了部分学生的劳动时间,并用得到的数据绘制成不完整的统计图表,如图所示:| 劳动时间(时) | 频数(人数) | 频率 |
| 0.5 | 12 | 0.12 |
| 1 | 30 | 0.3 |
| 1.5 | x | 0.4 |
| 2 | 18 | y |
| 合计 | m | 1 |
(2)求所有被调查同学的平均劳动时间.
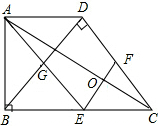 已知:在梯形ABCD中.AD∥BC,∠ABC=90°,∠BDC=90°,BC=2AD,E,F分别是BC、DC的中点.连接AE、EF、AC,连接BD,交AE于点G.
已知:在梯形ABCD中.AD∥BC,∠ABC=90°,∠BDC=90°,BC=2AD,E,F分别是BC、DC的中点.连接AE、EF、AC,连接BD,交AE于点G.
 如图,在平面直角坐标系xOy中,四边形OABC是矩形,点A(4,0),C(0,3).直线y=$\frac{1}{2}x$由原点开始向上平移,所得的直线y=$-\frac{1}{2}x+b$与矩形两边分别交于M、N两点,设△OMN面积为S,那么能表示S与b函数关系的图象大致是( )
如图,在平面直角坐标系xOy中,四边形OABC是矩形,点A(4,0),C(0,3).直线y=$\frac{1}{2}x$由原点开始向上平移,所得的直线y=$-\frac{1}{2}x+b$与矩形两边分别交于M、N两点,设△OMN面积为S,那么能表示S与b函数关系的图象大致是( )