题目内容
9.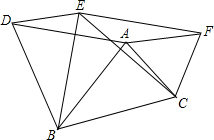 如图,在△ABC中,AB=4,AC=3,BC=5,以三边为边,在BC的同侧分别作三个等边三角形即△ABD,△BCE,△ACF.
如图,在△ABC中,AB=4,AC=3,BC=5,以三边为边,在BC的同侧分别作三个等边三角形即△ABD,△BCE,△ACF.(1)求证:四边形EFAD是平行四边形;
(2)求四边形EFAD的面积.
分析 (1)四边形EFAD平行四边形.根据△ABD,△EBC都是等边三角形容易得到全等条件证明△DBE≌△ABC,然后利用全等三角形的性质和平行四边形的判定可以证明四边形EFAD平行四边形;
(2)由勾股定理逆定理得出△ABC为直角三角形,算出∠DAF=150°,进一步得出∠AFE=30°,作AG⊥EF于点G,求得AG,求得面积即可.
解答 (1)证明:∵△ABD,△EBC都是等边三角形.
∴AD=BD=AB,BC=BE=EC
∠DBA=∠EBC=60°
∴∠DBE+∠EBA=∠ABC+∠EBA.
∴∠DBE=∠ABC.
在△DBE和△ABC中,
$\left\{\begin{array}{l}{BD=BA}\\{∠DBE=∠ABC}\\{BE=BC}\end{array}\right.$,
∴△DBE≌△ABC.
∴DE=AC.
又∵△ACF是等边三角形,
∴AC=AF.
∴DE=AF.
同理可证:AD=EF,
∴四边形EFAD平行四边形.
(2)解:∵在△ABC中,AB=4,AC=3,BC=5,
∴AB2+AC2=BC2,
∴△ABC为直角三角形,则∠BAC=90°,
∴∠DAF=150°,
∵AD∥EF,
∴∠AFE=30°,
作AG⊥EF于点G,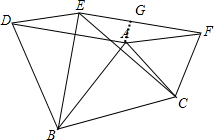
∴AG=$\frac{1}{2}$AF=$\frac{3}{2}$,
∴四边形EFAD的面积=AD•AG=6.
点评 此题考查平行四边形的判定与性质,等边三角形的性质,全等三角形的判定与性质,结合图形,灵活运用已知条件解决问题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目

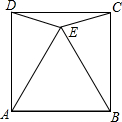 如图所示,点E是正方形ABCD内一点,EA=AB=BE,求∠DEC的度数.
如图所示,点E是正方形ABCD内一点,EA=AB=BE,求∠DEC的度数.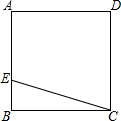 如图,ABCD是一块正方形的场地,小华和小芳在AB边上选定了一点E,测量知EC=30m,EB=10m,这块场地的面积和对角线长分别是多少?
如图,ABCD是一块正方形的场地,小华和小芳在AB边上选定了一点E,测量知EC=30m,EB=10m,这块场地的面积和对角线长分别是多少?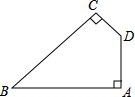 如图,在四边形ABCD中,∠A=∠C=90°,∠B=45°.AB=2$\sqrt{7}$,CD=$\sqrt{5}$,求四边形ABCD的面积.
如图,在四边形ABCD中,∠A=∠C=90°,∠B=45°.AB=2$\sqrt{7}$,CD=$\sqrt{5}$,求四边形ABCD的面积.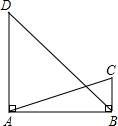 如图,已知∠ABC=∠BAD=90°,AC=13,BC=5,AD=16,求BD的长.
如图,已知∠ABC=∠BAD=90°,AC=13,BC=5,AD=16,求BD的长.