题目内容
7.已知方程x2+6x+n=0可以配方成(x+m)2=5,则以m、n为两边长的直角三角形的第三边的长为$\sqrt{34}$或4.分析 由配方得出m和n的值,再分情况讨论,即5的边是斜边还是直角边,由勾股定理求出第三边长即可.
解答 解:∵方程x2+6x+n=0配方得:(x+3)2=9-n,(x+m)2=5,
∴m=3,9-n=5,
∴n=4,
∴两边长为3和5,
当均为直角边时,
∴由勾股定理得:第三边长=$\sqrt{{3}^{2}+{5}^{2}}$=$\sqrt{34}$;
当5为斜边时,第三边长=$\sqrt{{5}^{2}-{3}^{2}}$=4;
综上所述:以m、n为两边长的直角三角形的第三边的长为$\sqrt{34}$或4.
故答案为:$\sqrt{34}$或4.
点评 此题主要考查了勾股定理以及配方法;通过配方法求出m和n,正确应用勾股定理分两种情况是解题关键.

练习册系列答案
相关题目
17. 如图所示,点E在AC的延长线上,下列条件不能判定AB∥CD的是( )
如图所示,点E在AC的延长线上,下列条件不能判定AB∥CD的是( )
 如图所示,点E在AC的延长线上,下列条件不能判定AB∥CD的是( )
如图所示,点E在AC的延长线上,下列条件不能判定AB∥CD的是( )| A. | ∠1=∠2 | B. | ∠3=∠4 | C. | ∠A=∠DCE | D. | ∠A+∠2+∠4=180° |
2. 如图,在等腰△ABC中,AB=AC,BD⊥AC,∠ABC=72°,则∠ABD等于( )
如图,在等腰△ABC中,AB=AC,BD⊥AC,∠ABC=72°,则∠ABD等于( )
 如图,在等腰△ABC中,AB=AC,BD⊥AC,∠ABC=72°,则∠ABD等于( )
如图,在等腰△ABC中,AB=AC,BD⊥AC,∠ABC=72°,则∠ABD等于( )| A. | 18° | B. | 36° | C. | 54° | D. | 64° |
12. 实数a,b,c,d在数轴上对应点的位置如图所示,这四个数中,倒数最大的是( )
实数a,b,c,d在数轴上对应点的位置如图所示,这四个数中,倒数最大的是( )
 实数a,b,c,d在数轴上对应点的位置如图所示,这四个数中,倒数最大的是( )
实数a,b,c,d在数轴上对应点的位置如图所示,这四个数中,倒数最大的是( )| A. | b | B. | d | C. | a | D. | c |
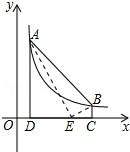 如图,点A(m,6)、B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.
如图,点A(m,6)、B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5. 已知:如图,在△ABC中,AB=BC,D是AC中点,点O是AB上一点,⊙O过点B且与AC相切于点E,交BD于点G,交AB于点F.
已知:如图,在△ABC中,AB=BC,D是AC中点,点O是AB上一点,⊙O过点B且与AC相切于点E,交BD于点G,交AB于点F.


