题目内容
15. 已知:如图,在△ABC中,AB=BC,D是AC中点,点O是AB上一点,⊙O过点B且与AC相切于点E,交BD于点G,交AB于点F.
已知:如图,在△ABC中,AB=BC,D是AC中点,点O是AB上一点,⊙O过点B且与AC相切于点E,交BD于点G,交AB于点F.(1)求证:BE平分∠ABD;
(2)当BD=2,sinC=$\frac{1}{2}$时,求⊙O的半径.
分析 (1)连接OE,根据等腰三角形三线合一的性质和切线的性质得出OE⊥AC,BD⊥AC,证得OE∥BD,根据平行线的性质和等腰三角形的性质即可证得结论;
(2)根据sinC=$\frac{1}{2}$求出AB=BC=4,设⊙O 的半径为r,则AO=4-r,得出sinA=sinC=$\frac{1}{2}$,根据OE⊥AC,得出sinA=$\frac{OE}{OA}$=$\frac{r}{4-r}$=$\frac{1}{2}$,即可求出半径.
解答  (1)证明:连接OE,
(1)证明:连接OE,
∵AC与⊙O相切,
∴OE⊥AC,
∵AB=BC且D是BC中点,
∴BD⊥AC,
∴OE∥BD,
∴∠OEB=∠DBE,
∵OB=OE,
∴∠OBE=∠OEB,
∴∠ABE=∠DBE,
∴BE平分∠ABD;
(2)解∵BD=2,sinC=$\frac{1}{2}$,BD⊥AC,
∴BC=4,
∴AB=4,
设⊙O的半径为r,则AO=4-r
∵AB=BC,
∴∠C=∠A,
∴sinA=sinC=$\frac{1}{2}$,
∵AC与⊙O相切于点E,
∴OE⊥AC
∴sinA=$\frac{OE}{OA}$=$\frac{r}{4-r}$=$\frac{1}{2}$,
∴r=$\frac{4}{3}$.
点评 本题考查了切线的性质,等腰三角形三线合一的性质,平行线的性质和判定,等腰三角形的性质,解直角三角形等,解(1)小题的关键是求出OE∥BD,解(2)小题的关键是得出关于r的方程,题型较好,难度适中,用了方程思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.计算(a2)4的结果是( )
| A. | a5 | B. | a6 | C. | a8 | D. | a9 |
10.若1<x<2,则化简|x-3|-$\sqrt{{x}^{2}-2x+1}$的结果为( )
| A. | 2x-4 | B. | -2 | C. | 4-2x | D. | 2 |
20.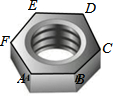 如图,螺母的一个面的外沿可以看作是正六边形,这个正六边形ABCDEF的半径是$2\sqrt{3}$cm,则这个正六边形的周长是( )
如图,螺母的一个面的外沿可以看作是正六边形,这个正六边形ABCDEF的半径是$2\sqrt{3}$cm,则这个正六边形的周长是( )
 如图,螺母的一个面的外沿可以看作是正六边形,这个正六边形ABCDEF的半径是$2\sqrt{3}$cm,则这个正六边形的周长是( )
如图,螺母的一个面的外沿可以看作是正六边形,这个正六边形ABCDEF的半径是$2\sqrt{3}$cm,则这个正六边形的周长是( )| A. | $6\sqrt{3}$cm | B. | 12cm | C. | $12\sqrt{3}$cm | D. | 36 cm |
 如图,已知EG∥AD,∠1=∠G,试说明AD平分∠BAC.
如图,已知EG∥AD,∠1=∠G,试说明AD平分∠BAC.