Question

18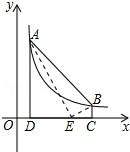．如图，点A（m，6）、B（n，1）在反比例函数图象上，AD⊥x轴于点D，BC⊥x轴于点C，DC=5．
（1）求反比例函数的解析式．
（2）点E在线段CD上，S_△ABE=10，求点E的坐标．

Answer 1

分析 （1）根据题意得到m与n的关系：n=6m，然后由DC=5，可得：n-m=5，进而可得：m=1，n=6，从而确定A，B两点的坐标，然后将A点的坐标代入y=$\frac{k}{x}$，即可求出k的值，进而可确定反比例函数的表达式；
（2）设E（x，0），表示出DE与CE，连接AE，BE，三角形ABE面积=四边形ABCD面积-三角形ADE面积-三角形BCE面积，求出即可．

解答 解：（1）设反比例函数的表达式为y=$\frac{k}{x}$，
∵A（m，6），B（n，1）在反比例函数上，
∴6m=n，
∵DC=5，
∴n-m=5，
解得：m=1，n=6，
∴A（1，6），B（6，1）
把A（1，6）代入y=$\frac{k}{x}$中，
解得：k=6
∴反比例函数表达式为y=$\frac{6}{x}$；
（2）设E（x，0），则DE=x-1，CE=6-x，
∵AD⊥x轴，BC⊥x轴，
∴∠ADE=∠BCE=90°，
连接AE，BE，
则S_△ABE=S_{四边形ABCD}-S_△ADE-S_△BCE=$\frac{1}{2}$（BC+AD）•DC-$\frac{1}{2}$DE•AD-$\frac{1}{2}$CE•BC=$\frac{1}{2}$×（1+6）×5-$\frac{1}{2}$（x-1）×6-$\frac{1}{2}$（6-x）×1=$\frac{35}{2}$-$\frac{5}{2}$x=10，
解得：x=3，
∴E（3，0）．

点评 此题考查了待定系数法求一次函数和反比例函数解析式，反比例函数图象上点的坐标特征，熟练掌握待定系数法是解本题的关键．