题目内容
19.(1)解不等式组$\left\{\begin{array}{l}{3(x-2)+4<5x}\\{\frac{1-x}{4}+x≥2x-1}\end{array}\right.$.(2)已知反比例函数y=$\frac{k}{x}$与一次函数y=2x+k的图象的一个交点的纵坐标是-4,求k的值.
分析 (1)先求出各个不等式的解集,然后求两者的公共部分.
(2)将y=-4分别代入两个函数中,然后解方程组即可求出k的值.
解答 解:(1)$\left\{\begin{array}{l}{3(x-2)+4<5x①}\\{\frac{1-x}{4}+x≥2x-1②}\end{array}\right.$
由①得,x>-1;
由②得,x≤1,
故不等式组的解集为:-1<x≤1;
(2)把y=-4代入y=$\frac{k}{x}$与y=2x+k得$\left\{\begin{array}{l}{-4=\frac{k}{x}}\\{-4=2x+k}\end{array}\right.$,
解得k=-8.
点评 本题考查了解一元一次不等式组,反比例函数和一次函数的交点问题,运用了函数知识和解方程组的内容,体现了方程思想.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
10.若1<x<2,则化简|x-3|-$\sqrt{{x}^{2}-2x+1}$的结果为( )
| A. | 2x-4 | B. | -2 | C. | 4-2x | D. | 2 |
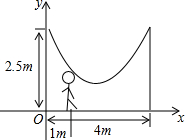 如图,小明的爸爸在相距4m的两树等高位置处拴了一根绳子,做成一个简易的秋千,绳子自然下垂呈抛物线,已知身高1.5m的小明站在距离树1m的地方,头部刚好触到绳子.
如图,小明的爸爸在相距4m的两树等高位置处拴了一根绳子,做成一个简易的秋千,绳子自然下垂呈抛物线,已知身高1.5m的小明站在距离树1m的地方,头部刚好触到绳子.