题目内容
15．
如图，点A是菱形ABCD的对角线BE的延长线上一点，则图中的全等三角形有（ ）对．| A． | 2 | B． | 3 | C． | 4 | D． | 5 |
分析 连结CD，如图，根据菱形的性质得BE垂直平分CD，则AC=AD，且BD=DE=CE=BC，然后根据“SSS”可判断△ACE≌△ADE，△ACB≌△ADB，△ECB≌△EDB．
解答 解：连结CD，如图，
∵四边形BDEC为菱形，
∴BE垂直平分CD，BD=DE=CE=BC，
∴AC=AD，
∴△ACE≌△ADE（SSS），△ACB≌△ADB（SSS），△ECB≌△EDB（SSS）．
故选B．
点评 本题考查了菱形的性质：菱形具有平行四边形的一切性质；菱形的四条边都相等；菱形的两条对角线互相垂直，并且每一条对角线平分一组对角；菱形是轴对称图形，它有2条对称轴，分别是两条对角线所在直线．也考查了全等三角形的判定．
练习册系列答案
考前必练系列答案
相关题目
3．二次函数y=ax2+bx+c（a，b，c为常数，且a≠0）中的x与y的部分对应值如表：
下列结论：①c=3；②当x＞1时，y的值随x的增大而减小；③函数的最大值是5；④ac＜0．其中正确的个数为 （ ）
| x | -1 | 0 | 1 | 3 |
| y | -1 | 3 | 5 | 3 |
| A． | 4个 | B． | 3个 | C． | 2个 | D． | 1个 |
10．方程2x2-4=0的解是（ ）
| A． | x=2 | B． | x=-2 | C． | x=±2 | D． | x=$±\sqrt{2}$ |
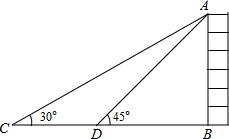如图，某校数学兴趣小组在大厦前的平地上C处，测得大厦顶端A的仰角∠ACB=30°，在D处测得大厦顶端A的仰角∠ADB=45°，那么从点A观察C、D处的视角∠CAD的度数为（ ）