题目内容
17.(1)$\frac{\sqrt{72}-\sqrt{16}}{\sqrt{8}}$-($\sqrt{3}$+$\sqrt{2}$)($\sqrt{3}$-$\sqrt{2}$)(2)${({π-1})^0}+{({\frac{{\sqrt{3}}}{2}})^{-1}}+|{5-\sqrt{27}}|-\sqrt{{{10}^2}-{6^2}}$.
分析 (1)利用二次根式的除法法则和平方差公式计算;
(2)根据零指数幂和负整数指数幂的意义得到原式=1+$\frac{2}{\sqrt{3}}$+3$\sqrt{3}$-5-$\sqrt{64}$,然后化简后合并即可.
解答 解:(1)原式=$\sqrt{\frac{72}{8}}$-$\sqrt{\frac{16}{8}}$-(3-2)
=3-$\sqrt{2}$-1
=2-$\sqrt{2}$;
(2)原式=1+$\frac{2}{\sqrt{3}}$+3$\sqrt{3}$-5-$\sqrt{64}$
=1+$\frac{2\sqrt{3}}{3}$+3$\sqrt{3}$-5-8
=$\frac{11\sqrt{3}}{3}$-12.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了零指数幂和负整数指数幂.

练习册系列答案
相关题目
6.下面四个式子中正确的是( )
| A. | -$\frac{1}{5}$<-5<5 | B. | 5<-5<-$\frac{1}{5}$ | C. | -5<5<-$\frac{1}{5}$ | D. | -5<-$\frac{1}{5}$<5 |
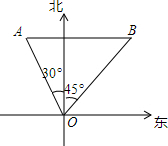 如图,某海防哨所(O)发现在它的北偏西30°,距离为500m的A处有一艘船,该船向正东方向航行,经过3min到达哨所东北方向的B处,则该船的航速为每小时13.7km.(精确到0.1)
如图,某海防哨所(O)发现在它的北偏西30°,距离为500m的A处有一艘船,该船向正东方向航行,经过3min到达哨所东北方向的B处,则该船的航速为每小时13.7km.(精确到0.1)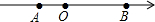 已知数轴上A,B对应的实数为a,b,化简代数式:|a-b|-$\sqrt{(b-a)^{2}}$+$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$=b-a.
已知数轴上A,B对应的实数为a,b,化简代数式:|a-b|-$\sqrt{(b-a)^{2}}$+$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$=b-a.