题目内容
14.请你设计一个摸球游戏,要求:(1)袋子中要有黄球、绿球和红球三种球.
(2)摸到球的概率;P(摸到红球)=$\frac{1}{4}$;P(摸到黄球)=$\frac{2}{3}$;
并求出摸到绿球的概率有多大?
分析 先求出各分母的最小公倍数12,再设计一个摸球游戏:在一不透明的袋中,装有12个黄球、绿球和红球,其中红球3个、黄球8个,他们除了颜色外都相同,任意从中摸出一个球,则P(摸到红球)=$\frac{1}{4}$;P(摸到黄球)=$\frac{2}{3}$;然后根据概率公式即可求出摸到绿球的概率.
解答 解:由题意,可设计一个摸球游戏:在一不透明的袋中,装有12个黄球、绿球和红球,其中红球3个、黄球8个,他们除了颜色外都相同.
∵绿球有:12-3-8=1个,
∴任意从中摸出一个球,则P(摸到绿球)=$\frac{1}{12}$.
点评 此题考查了概率公式的应用.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
9.已知x+y=8,xy=5,则x2+y2的值是( )
| A. | 84 | B. | 74 | C. | 64 | D. | 54 |
6.若x<0,则化简$\sqrt{{-x}^{3}y}$的结果是( )
| A. | -x$\sqrt{xy}$ | B. | x$\sqrt{-xy}$ | C. | -x$\sqrt{-xy}$ | D. | x$\sqrt{xy}$ |
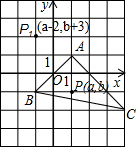 如图所示,三角形ABC中,任意一点P(a,b)经平移后对应点P(a-2,b+3),将△ABC作同样的平移得到△A1B1C1.
如图所示,三角形ABC中,任意一点P(a,b)经平移后对应点P(a-2,b+3),将△ABC作同样的平移得到△A1B1C1.