题目内容
2.(1)如图(a),已知AB∥CD,∠B=120°,∠C=25°.①求α的度数;
②若∠B=m°,∠C=n°,请直接写出α与m,n之间的关系式;
(2)如图(b),已知AB∥EF,∠BCD=90°,试探究α、β、θ之间的数量关系,并说明理由.
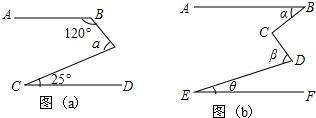
分析 (1)延长BE交CD于F,根据平行线的性质和数据线的外角的性质即可解答;
(2)作CG∥AB,DH∥AB,根据两直线平行,内错角相等计算即可.
解答  解:如图a,(1)①延长BE交CD于F,
解:如图a,(1)①延长BE交CD于F,
∵AB∥CD,∠B=120°,
∴∠EFC=180°-∠B=60°,
∵∠C=25°,
∴α=∠EFC+∠C=85°;
②同理,∠EFC=180°-∠B=180°-m,
α=∠EFC+∠C=180°-m+n;
(2) α+β-θ=90°,
α+β-θ=90°,
证明:如图b,作CG∥AB,DH∥AB,
∵AB∥EF,∴DH∥EF,CG∥DH,
∴∠BCG=∠ABC,∠HDE=∠DEF,∠GCD=∠CDH,
∴∠BCD=∠ABC+∠CDH,即90°=α+β-θ.
点评 本题考查的是平行线的性质,掌握两直线平行,同位角相等、内错角相等和同旁内角互补是解题的关键,注意辅助线的作法是重点.

练习册系列答案
相关题目
9. 如图是由四个相同的小正方体组成的立体图形,它的左视图为( )
如图是由四个相同的小正方体组成的立体图形,它的左视图为( )
 如图是由四个相同的小正方体组成的立体图形,它的左视图为( )
如图是由四个相同的小正方体组成的立体图形,它的左视图为( )| A. |  | B. |  | C. |  | D. |  |
13.先化简,后求值:($\frac{x}{x-1}$-$\frac{x}{{x}^{2}-1}$)÷$\frac{{x}^{2}-x}{{x}^{2}-2x+1}$,然后选一个合适的x的值代入求值.
7.下列计算中,正确的是( )
| A. | (-5)-(-3)=-8 | B. | (+5)-(3)=2 | C. | (+7)-(+8)=-1 | D. | (-5)-|-5|=0 |
12. 如图所示,在图形B到图形A的变化过程中,下列描述正确的是( )
如图所示,在图形B到图形A的变化过程中,下列描述正确的是( )
 如图所示,在图形B到图形A的变化过程中,下列描述正确的是( )
如图所示,在图形B到图形A的变化过程中,下列描述正确的是( )| A. | 向上平移2个单位,向左平移4个单位 | |
| B. | 向上平移1个单位,向左平移4个单位 | |
| C. | 向上平移2个单位,向左平移5个单位 | |
| D. | 向上平移1个单位,向左平移5个单位 |
 如图,直线AB分别交EF、BC于点A、B,AC平分∠BAE,∠ABC=76°,∠GAF=52°,EF与BC平行吗?请说明理由.
如图,直线AB分别交EF、BC于点A、B,AC平分∠BAE,∠ABC=76°,∠GAF=52°,EF与BC平行吗?请说明理由.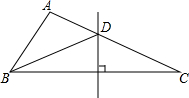 如图,△ABC中,∠A=100°,BC的垂直平分线交AC于点D,且∠ABD:∠DBC=4:3,则∠C的度数等于24°.
如图,△ABC中,∠A=100°,BC的垂直平分线交AC于点D,且∠ABD:∠DBC=4:3,则∠C的度数等于24°. 中国•宜春2015年首届栀子节生态旅游节于5月16日在宜春市袁州区洪塘镇开幕,记者小刚从家里出发去生态园采访,途中发现忘带小记者证,赶紧往家里打电话,妈妈接到电话后立即带上记者证赶往生态园,同时小刚原路返回;两人相遇后,小刚立即赶往生态园,妈妈回家,15分钟妈妈到家,再经过3分钟小刚到达生态园,小刚始终以100米的速度步行,小刚和妈妈的距离y(单位:米)与小刚打完电话后的步行时间t(单位:分)之间的函数关系如图所示,根据图象信息回答下列问题:
中国•宜春2015年首届栀子节生态旅游节于5月16日在宜春市袁州区洪塘镇开幕,记者小刚从家里出发去生态园采访,途中发现忘带小记者证,赶紧往家里打电话,妈妈接到电话后立即带上记者证赶往生态园,同时小刚原路返回;两人相遇后,小刚立即赶往生态园,妈妈回家,15分钟妈妈到家,再经过3分钟小刚到达生态园,小刚始终以100米的速度步行,小刚和妈妈的距离y(单位:米)与小刚打完电话后的步行时间t(单位:分)之间的函数关系如图所示,根据图象信息回答下列问题: