题目内容
6.若x<0,则化简$\sqrt{{-x}^{3}y}$的结果是( )| A. | -x$\sqrt{xy}$ | B. | x$\sqrt{-xy}$ | C. | -x$\sqrt{-xy}$ | D. | x$\sqrt{xy}$ |
分析 首先判断出当x<0时,-x>0,然后根据化简二次根式的步骤,求出化简$\sqrt{{-x}^{3}y}$的结果是多少即可.
解答 解:当x<0时,-x>0,
$\sqrt{{-x}^{3}y}$=$\sqrt{{(-x)}^{2}•(-xy)}$=-x$\sqrt{-xy}$.
故选:C.
点评 此题主要考查了二次根式的性质和化简,要熟练掌握,解答此题的关键是要明确化简二次根式的步骤:①把被开方数分解因式;②利用积的算术平方根的性质,把被开方数中能开得尽方的因数(或因式)都开出来;③化简后的二次根式中的被开方数中每一个因数(或因式)的指数都小于根指数2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.下列各式中,计算正确的是( )
| A. | $\sqrt{(-16)(-81)}$=$\sqrt{-16}×\sqrt{-81}$=(-4)×(-9)=36 | B. | 2$\sqrt{5}$×3$\sqrt{5}$=6$\sqrt{5}$ | ||
| C. | $\sqrt{-25}$×$\sqrt{-125}$=$\sqrt{(-25)(-125)}$ | D. | $\sqrt{25×121}$=$\sqrt{25}$×$\sqrt{121}$=5×11=55 |
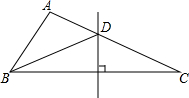 如图,△ABC中,∠A=100°,BC的垂直平分线交AC于点D,且∠ABD:∠DBC=4:3,则∠C的度数等于24°.
如图,△ABC中,∠A=100°,BC的垂直平分线交AC于点D,且∠ABD:∠DBC=4:3,则∠C的度数等于24°.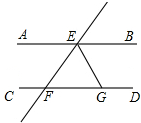 已知:如图,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠BEF,若∠EFD=72°,则∠EGC等于多少度?
已知:如图,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠BEF,若∠EFD=72°,则∠EGC等于多少度? 中国•宜春2015年首届栀子节生态旅游节于5月16日在宜春市袁州区洪塘镇开幕,记者小刚从家里出发去生态园采访,途中发现忘带小记者证,赶紧往家里打电话,妈妈接到电话后立即带上记者证赶往生态园,同时小刚原路返回;两人相遇后,小刚立即赶往生态园,妈妈回家,15分钟妈妈到家,再经过3分钟小刚到达生态园,小刚始终以100米的速度步行,小刚和妈妈的距离y(单位:米)与小刚打完电话后的步行时间t(单位:分)之间的函数关系如图所示,根据图象信息回答下列问题:
中国•宜春2015年首届栀子节生态旅游节于5月16日在宜春市袁州区洪塘镇开幕,记者小刚从家里出发去生态园采访,途中发现忘带小记者证,赶紧往家里打电话,妈妈接到电话后立即带上记者证赶往生态园,同时小刚原路返回;两人相遇后,小刚立即赶往生态园,妈妈回家,15分钟妈妈到家,再经过3分钟小刚到达生态园,小刚始终以100米的速度步行,小刚和妈妈的距离y(单位:米)与小刚打完电话后的步行时间t(单位:分)之间的函数关系如图所示,根据图象信息回答下列问题: