题目内容
13. 如图,抛物线y=ax2+bx+c的开口向下,与x轴和y轴分别交于点A(-4,0)和点B(0,2),过点B作BC⊥AB交抛物线于点C,连接AC,且∠BAC=∠BAO.
如图,抛物线y=ax2+bx+c的开口向下,与x轴和y轴分别交于点A(-4,0)和点B(0,2),过点B作BC⊥AB交抛物线于点C,连接AC,且∠BAC=∠BAO.(1)求BC的长;
(2)求抛物线的解析式.
分析 (1)根据勾股定理,可得AB的长,根据相似三角形的判定与性质,可得答案;
(2)根据两点间的距离,可得两个方程,根据解方程,可得C点坐标,根据待定系数法,可得函数解析式.
解答 解:(1)在Rt△AOB中,由勾股定理,得
AB=$\sqrt{{AO}^{2}{+BO}^{2}}$=2$\sqrt{5}$.
∵BC⊥AB,
∴∠ABC=∠AOB=90°,
∵∠CAB=∠BAO,
∴△CAB∽△BAO,
$\frac{BC}{BO}$=$\frac{AB}{AO}$,即$\frac{BC}{2}$=$\frac{2\sqrt{5}}{4}$,
BC=$\sqrt{5}$;
(2)设C点坐标为(m,n),由勾股定理,
AC=$\sqrt{{AB}^{2}{+BC}^{2}}$=5.
AC2=25,BC2=5,
即$\left\{\begin{array}{l}{{(m+4)}^{2}{+n}^{2}=25}\\{\;}\\{{m}^{2}{+(n-2)}^{2}=5}\end{array}\right.$,
解得m=-1,m=1(舍),n=4,
即C点坐标(-1,4).
将A,B,C点坐标代入函数解析式,得
$\left\{\begin{array}{l}{a-b+c=4}\\{16a-4b+c=0}\\{c=2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-\frac{5}{6}}\\{b=-\frac{17}{6}}\\{c=2}\end{array}\right.$,
抛物线的解析式为y=-$\frac{5}{6}$x2-$\frac{17}{6}$x+2.
点评 本题考查了二次函数综合题,解(1)的关键是利用相似三角形的判定与性质;解(2)的关键是利用两点间的距离求出C点坐标,又利用了待定系数法.

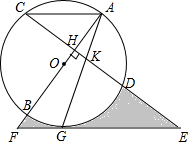 如图,AB是⊙O的直径,弦CD⊥AB于H,G为⊙O上一点,AG交CD于K,E为CD延长线上一点,且EK=EG,EG的延长线交AB的延长线于F.
如图,AB是⊙O的直径,弦CD⊥AB于H,G为⊙O上一点,AG交CD于K,E为CD延长线上一点,且EK=EG,EG的延长线交AB的延长线于F.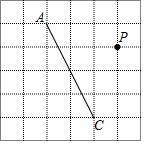 如图,在方格纸中每个小正方形的边长均为1,线段AC的两个端点均在小正方形的顶点上.
如图,在方格纸中每个小正方形的边长均为1,线段AC的两个端点均在小正方形的顶点上.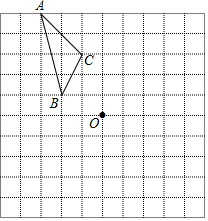 如图,在边长为1个单位长度的小正方形网格中,给出了△ABC(顶点是网格线的交点).
如图,在边长为1个单位长度的小正方形网格中,给出了△ABC(顶点是网格线的交点).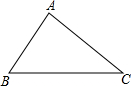 如图,在△ABC中,∠B=55°,∠C=40°,直线MN垂直平分AC,交BC于点D,连接AD.
如图,在△ABC中,∠B=55°,∠C=40°,直线MN垂直平分AC,交BC于点D,连接AD.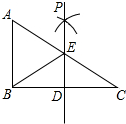 如图,已知在Rt△ABC中,∠ABC=90°,点D是BC边的中点,分别以B、C为圆心,大于线段BC长度一半的长为半径画弧,两弧在直线BC上方的交点为P,直线PD交AC于点E,连接BE,则下列结论:①ED⊥BC;②∠A=∠EBA;③EB平分∠AED;④ED=$\frac{1}{2}$AB中,一定正确的是①②④.(写序号)
如图,已知在Rt△ABC中,∠ABC=90°,点D是BC边的中点,分别以B、C为圆心,大于线段BC长度一半的长为半径画弧,两弧在直线BC上方的交点为P,直线PD交AC于点E,连接BE,则下列结论:①ED⊥BC;②∠A=∠EBA;③EB平分∠AED;④ED=$\frac{1}{2}$AB中,一定正确的是①②④.(写序号)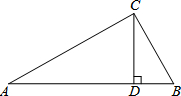 如图在△ABC中,CD是AB上的高且CD2=AD•BD,求证:△ABC是直角三角形.
如图在△ABC中,CD是AB上的高且CD2=AD•BD,求证:△ABC是直角三角形.