题目内容
3.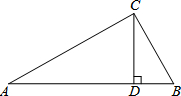 如图在△ABC中,CD是AB上的高且CD2=AD•BD,求证:△ABC是直角三角形.
如图在△ABC中,CD是AB上的高且CD2=AD•BD,求证:△ABC是直角三角形.
分析 根据条件可以求出△ADC∽△CDB就可以得出∠A=∠DCB而得出结论.
解答 证明:∵CD2=AD•BD,
∴$\frac{CD}{AD}=\frac{BD}{CD}$.
∵CD⊥AB,
∴∠ADC=∠BDC=90°,
∴△ADC∽△CDB,
∴∠A=∠DCB.
∵∠A+∠ACD=90°,
∴∠BCD+∠ACD=90°,
即∠ACB=90°.
∴△ABC是直角三角形.
点评 本题考查了相似三角形的判定与性质的运用,解答时证明三角形相似是关键.

练习册系列答案
相关题目
18.数学兴趣小组的小颖想测量教学楼前的一棵树的高度,下午课外活动时她测得一根长为1米的竹竿的影长是0.8米,测树高时,这棵树在地面上影长为2.6米,请计算树高为( )米.
| A. | 3.25 | B. | 4.25 | C. | 4.45 | D. | 4.75 |
14.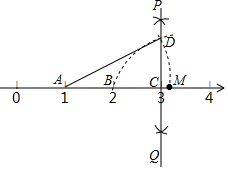 如图,数轴上点A、B、C分别对应1、2、3,过点C作PQ⊥AB,以点C为圆心,BC长为半径画弧,交PQ于点D,以点A为圆心,AD长为半径画弧,交数轴于点M,则点M对应的数是( )
如图,数轴上点A、B、C分别对应1、2、3,过点C作PQ⊥AB,以点C为圆心,BC长为半径画弧,交PQ于点D,以点A为圆心,AD长为半径画弧,交数轴于点M,则点M对应的数是( )
 如图,数轴上点A、B、C分别对应1、2、3,过点C作PQ⊥AB,以点C为圆心,BC长为半径画弧,交PQ于点D,以点A为圆心,AD长为半径画弧,交数轴于点M,则点M对应的数是( )
如图,数轴上点A、B、C分别对应1、2、3,过点C作PQ⊥AB,以点C为圆心,BC长为半径画弧,交PQ于点D,以点A为圆心,AD长为半径画弧,交数轴于点M,则点M对应的数是( )| A. | $\sqrt{3}$+1 | B. | $\sqrt{5}$+1 | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
 如图,抛物线y=ax2+bx+c的开口向下,与x轴和y轴分别交于点A(-4,0)和点B(0,2),过点B作BC⊥AB交抛物线于点C,连接AC,且∠BAC=∠BAO.
如图,抛物线y=ax2+bx+c的开口向下,与x轴和y轴分别交于点A(-4,0)和点B(0,2),过点B作BC⊥AB交抛物线于点C,连接AC,且∠BAC=∠BAO.