题目内容
16.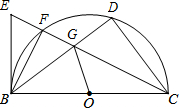 如图,直径为10的半圆O,tan∠DBC=$\frac{3}{4}$,∠BCD的平分线交⊙O于F,E为CF延长线上一点,且∠EBF=∠GBF.
如图,直径为10的半圆O,tan∠DBC=$\frac{3}{4}$,∠BCD的平分线交⊙O于F,E为CF延长线上一点,且∠EBF=∠GBF.(1)求证:BE为⊙O切线;
(2)求证:BG2=FG•CE;
(3)求OG的值.
分析 (1)根据圆周角定理得到∠FBD=∠DCF,由角平分线的定义得到∠BCF=∠DCF,等量代换得到∠EBF=∠∠BCF,推出BE⊥BC,即可得到结论;
(2)证明:由(1)知∠BFC=∠EBC=90°,∠EBF=∠ECB,通过相似三角形的性质得到BE2=EF•CE,得到∠BFE=∠BFG=90°,推出△BEF≌△BGF,根据全等三角形的性质得到BE=BG,EF=FG,等量代换得到结论;
(3)如图,过G作GH⊥BC于H,根据角平分线的性质得到GH=GD,根据三角函数的定义得到$\frac{GH}{BG}=\frac{GD}{8-GD}$=$\frac{3}{5}$,求得GD=GH=3,BG=5,BH=4,根据勾股定理即可得到结论.
解答 (1)证明:由同弧所对的圆周角相等得∠FBD=∠DCF,
又∵CF平分∠BCD,
∴∠BCF=∠DCF,
已知∠EBF=∠GBF,
∴∠EBF=∠∠BCF,
∵BC为⊙O直径,
∴∠BFC=90°,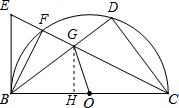
∴∠FBC+∠FCB=90°,
∴∠FBC+∠EBF=90°,
∴BE⊥BC,
∴BE为⊙O切线;
(2)证明:由(1)知∠BFC=∠EBC=90°,∠EBF=∠ECB,
∴△BEF∽△CEB,
∴BE2=EF•CE,
又∠EBF=∠GBF,BF⊥EG,
∴∠BFE=∠BFG=90°,
在△BEF与△BGF中,$\left\{\begin{array}{l}{∠EBF=∠GBF}\\{BF=BF}\\{∠EFB=∠BFG}\end{array}\right.$,
∴△BEF≌△BGF,
∴BE=BG,EF=FG,
∴BG2=FG•CE;
(3)如图,过G作GH⊥BC于H,
∵CF平分∠BCD,
∴GH=GD,
∵tan∠DBC=$\frac{3}{4}$,
∴sin∠DBC=$\frac{3}{5}$,
∵BC=10,
∴BD=8,BG=BD-GD=8-GD,
∴$\frac{GH}{BG}=\frac{GD}{8-GD}$=$\frac{3}{5}$,
∴GD=GH=3,BG=5,BH=4,
∵BC=10,∴OH=OB-BH=1,
在Rt△OGH中,由勾股定理得OG=$\sqrt{10}$.
点评 本题考查了相似三角形的判定和性质,圆周角定理,全等三角形的判定和性质,切线的判定,角平分线的性质,三角函数的定义,作GH⊥BC是解决(3)小题的关键.

 步步高达标卷系列答案
步步高达标卷系列答案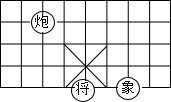 如图所示,若在某棋盘上建立直角坐标系,使“将”位于点(2,-2),“象”位于点(4,-2),则“炮”位于点( )
如图所示,若在某棋盘上建立直角坐标系,使“将”位于点(2,-2),“象”位于点(4,-2),则“炮”位于点( )| A. | (1,3) | B. | (0,1) | C. | (-1,2) | D. | (-2,2) |
| A. | k=-1 | B. | k=1 | C. | k=±1 | D. | k≠0 |
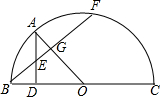 如图所示,BC是半圆O的直径,AD⊥BC,垂足为D,AB弧长等于AF弧长,BF与AD、AO分别交于点E、G.
如图所示,BC是半圆O的直径,AD⊥BC,垂足为D,AB弧长等于AF弧长,BF与AD、AO分别交于点E、G.
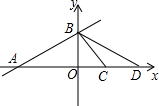 已知一次函数y=$\frac{{\sqrt{2}}}{3}$x+$\sqrt{2}$的图象与x轴,y轴,分别交于A、B两点,点C坐标为(1,0),点D在x轴上,且∠BCD和∠ABD是两个不相等的钝角,求经过B、D两点的一次函数的解析式.
已知一次函数y=$\frac{{\sqrt{2}}}{3}$x+$\sqrt{2}$的图象与x轴,y轴,分别交于A、B两点,点C坐标为(1,0),点D在x轴上,且∠BCD和∠ABD是两个不相等的钝角,求经过B、D两点的一次函数的解析式.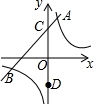 如图,一次函数y=x+3的图象与反比例函数y=$\frac{4}{x}$的图象交于A,B两点,与y轴交于点C,C点关于x轴的对称点是D点,则△ABD的面积是15.
如图,一次函数y=x+3的图象与反比例函数y=$\frac{4}{x}$的图象交于A,B两点,与y轴交于点C,C点关于x轴的对称点是D点,则△ABD的面积是15.