题目内容
16.在△ABC中,点D是AB边上一点(不与AB重合),AD=kBD,过点D作∠EDF+∠C=180°,与CA、CB分别交于E、F.(1)如图1,当DE=DF时,求$\frac{AC}{BC}$的值.
(2)如图2,若∠ACB=90°,∠B=30°,DE=m,求DF的长(用含k,m的式子表示)
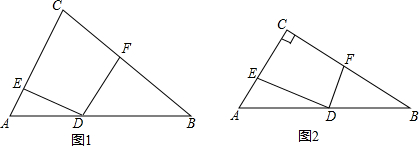
分析 (1)连接CD,由∠EDF+∠C=180°,推出D,E,C,F四点共圆,根据正弦定理得$\frac{AD}{sin∠ACD}=\frac{AC}{sin∠ADC}$ ①,$\frac{BD}{sin∠ADC}=\frac{BC}{sin∠BDC}$,②,①÷②得,$\frac{AD}{BD}=\frac{AC}{BC}$,根据AD=kBD,根据得到结论;
(2)根据三角形的内角和得到∠A=60°,根据正弦定理得:$\frac{AD}{sin∠DEA}=\frac{DE}{sin∠A}$=$\frac{DE}{\frac{\sqrt{3}}{2}}$ ③,$\frac{BD}{sin∠DFB}=\frac{DF}{sin∠B}=\frac{DF}{\frac{1}{2}}$,④,④÷③得:$\frac{\sqrt{3}DF}{DE}=\frac{BD}{AD}$,求得DF=$\frac{\sqrt{3}DE}{3}•\frac{BD}{AD}$,即可得到结论.
解答 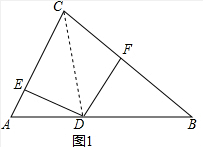 解:如图1,连接CD,
解:如图1,连接CD,
∵∠EDF+∠C=180°,
∴D,E,C,F四点共圆,
∵DE=DF,
∴∠DCE=∠DCF,
根据正弦定理得$\frac{AD}{sin∠ACD}=\frac{AC}{sin∠ADC}$ ①,
$\frac{BD}{sin∠DCB}=\frac{BC}{sin∠BDC}$,
∴$\frac{BD}{sin∠ADC}=\frac{BC}{sin∠BDC}$,②,
∵∠ADC=180°-∠BDC,
∴sin∠ADC=sin∠BDC,
①÷②d得,$\frac{AD}{BD}=\frac{AC}{BC}$,
∵AD=kBD,
∴$\frac{AC}{BC}$=k;
(2)∵∠ACB=90°,∠B=30°,
∴∠A=60°,
根据正弦定理得:$\frac{AD}{sin∠DEA}=\frac{DE}{sin∠A}$=$\frac{DE}{\frac{\sqrt{3}}{2}}$ ③,$\frac{BD}{sin∠DFB}=\frac{DF}{sin∠B}=\frac{DF}{\frac{1}{2}}$,④,
由(1)知D,E,C,F四点共圆,
∴∠DEA+∠DFB=180°,
∴sin∠DEA=sin∠DFB,④÷③得:$\frac{\sqrt{3}DF}{DE}=\frac{BD}{AD}$,
∴DF=$\frac{\sqrt{3}DE}{3}•\frac{BD}{AD}$,
∵AD=kBD,DE=m,
∴DF=$\frac{\sqrt{3}m}{3k}$.
点评 本题考查了相似三角形的判定和性质,三角形的内角和,三角函数的定义,正弦定理,正确掌握正弦定理是解题的关键.

 备战中考寒假系列答案
备战中考寒假系列答案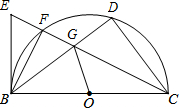 如图,直径为10的半圆O,tan∠DBC=$\frac{3}{4}$,∠BCD的平分线交⊙O于F,E为CF延长线上一点,且∠EBF=∠GBF.
如图,直径为10的半圆O,tan∠DBC=$\frac{3}{4}$,∠BCD的平分线交⊙O于F,E为CF延长线上一点,且∠EBF=∠GBF.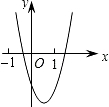 二次函数y=ax2+bx+c的图形如图所示,则一次函数y=ax-c与反比例函数y=$\frac{a+b+c}{x}$在同一坐标系内的图象大致为( )
二次函数y=ax2+bx+c的图形如图所示,则一次函数y=ax-c与反比例函数y=$\frac{a+b+c}{x}$在同一坐标系内的图象大致为( )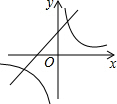
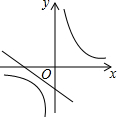
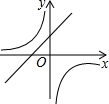
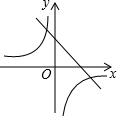
 如图,直线y=kx-1与x轴、y轴分别交与B、C两点,OC=2OB,点A是直线BC上一动点.
如图,直线y=kx-1与x轴、y轴分别交与B、C两点,OC=2OB,点A是直线BC上一动点.