题目内容
3．
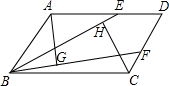已知：如图，在平行四边形ABCD中，E、F分别为边AD、CD上一点，且BE=BF，AG⊥BF于F，CH⊥BE于H，求证：AG=CH．
分析 连接CE、AF根据平行四边形的面积可得S△ABF=$\frac{1}{2}$S平行四边形ABCD=S△BCE，再根据三角形的面积公式可证出AG=CH．
解答 
证明：连接CE、AF，
∵S△ABF=$\frac{1}{2}$S平行四边形ABCD，S△BCE=$\frac{1}{2}$S平行四边形ABCD，
∴S△ABF=S△BCE，
∵S△ABF=$\frac{1}{2}$BF•AG，S△BCE=$\frac{1}{2}$BE•CH，
∵BE=BF，
∴AG=CH．
点评 此题主要考查了平行四边形的性质，关键是掌握平行四边形的面积=底×高．
练习册系列答案
小学课时作业全通练案系列答案
金版课堂课时训练系列答案
单元全能练考卷系列答案
相关题目
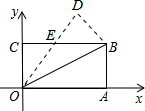如图，在矩形OABC中，OA=8，OC=4，沿对角线OB折叠后，点A与点D重合，OD与BC交于点E，试求点D的坐标．
在矩形ABCD中，点E是BC上一点，DF=DC，DF⊥AE，垂足为F．求证：AE=AD．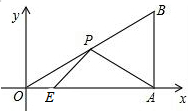
在平面直角坐标系中，Rt△OAB的顶点A在x轴上，点A的坐标为（3，0），∠AOB=30°，点E的坐标为（$\frac{1}{2}$，0），点P为斜边OB上的一个动点，则PA+PE的最小值为$\frac{\sqrt{31}}{2}$．
如图，在菱形ABCD中，边长为1，∠A=60°，顺次连结菱形ABCD各边中点，可得四边形A1B1C1D1；顺次连结四边形A1B1C1D1各边中点，可得四边形A2B2C2D2；顺次连结四边形A2B2C2D2各边中点，可得四边形A3B3C3D3；按此规律继续下去…，则四边形A2016B2016C2016D2016的面积是$\frac{\sqrt{3}}{{2}^{2017}}$．