题目内容
13. 如图,在菱形ABCD中,边长为1,∠A=60°,顺次连结菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去…,则四边形A2016B2016C2016D2016的面积是$\frac{\sqrt{3}}{{2}^{2017}}$.
如图,在菱形ABCD中,边长为1,∠A=60°,顺次连结菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去…,则四边形A2016B2016C2016D2016的面积是$\frac{\sqrt{3}}{{2}^{2017}}$.
分析 首先利用已知数据求出菱形ABCD的面积,易得四边形A2B2C2D2的面积等于矩形A1B1C1D1的面积的$\frac{1}{2}$,同理可得四边形A3B3C3D3的面积等于四边形A2B2C2D2的面积$\frac{1}{2}$,那么等于矩形A1B1C1D1的面积的($\frac{1}{2}$)2,同理可得四边形A2016B2016C2016D2016的面积.
解答 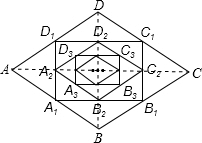 解:如图,连接AC、BD.则AC⊥BD.
解:如图,连接AC、BD.则AC⊥BD.
∵菱形ABCD中,边长为1,∠A=60°,
∴S菱形ABCD=$\frac{1}{2}$AC•BD=1×1×sin60°=$\sqrt{3}$
∵顺次连结菱形ABCD各边中点,可得四边形A1B1C1D1,
易证四边形A1B1C1D1 是矩形,
S矩形A1B1C1D1=$\frac{1}{2}$C•$\frac{1}{2}$BD=$\frac{1}{4}$AC•BD=$\frac{1}{2}$S菱形ABCD.
同理,S四边形A2B2C2D2=$\frac{1}{2}$S矩形A1B1C1D1=$\frac{1}{2}$S菱形ABCD,
S矩形A3B3C3D3=($\frac{1}{2}$)3S菱形ABCD.
四边形A2016B2016C2016D2016的面积是=$\frac{1}{{2}^{2017}}$S菱形ABCD=$\frac{\sqrt{3}}{{2}^{2017}}$,
故答案为:$\frac{\sqrt{3}}{{2}^{2017}}$.
点评 本题考查了菱形以及中点四边形的性质.找到中点四边形的面积与原四边形的面积之间的关系是解决本题的关键.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
1.若点A(-1,y1),B(1,y2),C(2,y3)都在反比例函数y=$\frac{k}{x}(k>0)$的图象上,则y1,y2,y3的大小关系为( )
| A. | y1<y3<y2 | B. | y1<y2<y3 | C. | y3<y2<y1 | D. | y3<y1<y2 |
2.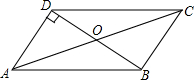 如图,在?ABCD中,∠ODA=90°,AC=20cm,BD=12cm,则AD的长为( )
如图,在?ABCD中,∠ODA=90°,AC=20cm,BD=12cm,则AD的长为( )
 如图,在?ABCD中,∠ODA=90°,AC=20cm,BD=12cm,则AD的长为( )
如图,在?ABCD中,∠ODA=90°,AC=20cm,BD=12cm,则AD的长为( )| A. | 8cm | B. | 10cm | C. | 12cm | D. | 16cm |
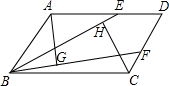 已知:如图,在平行四边形ABCD中,E、F分别为边AD、CD上一点,且BE=BF,AG⊥BF于F,CH⊥BE于H,求证:AG=CH.
已知:如图,在平行四边形ABCD中,E、F分别为边AD、CD上一点,且BE=BF,AG⊥BF于F,CH⊥BE于H,求证:AG=CH.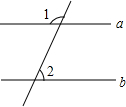 如图,a∥b,∠1=130°,则∠2=50°.
如图,a∥b,∠1=130°,则∠2=50°.