题目内容
9. 如图,在某段测速公路BC上(公路视为直线)交通管理部门规定汽车的最高行驶速度不能超过60千米/时,并在离该公路100米处设置了一个监测点A,已知点B在A的北偏西60°方向上,点C在点A的偏东40°方向上.(1)监测发现,一辆汽车从点B匀速行驶到点C所用时间为15秒.请你通过计算,判断该越野车在这段限速路上是否超速?(参考数据:sin40°=0.64,tan40°=0.84,$\sqrt{3}$=1.73)
如图,在某段测速公路BC上(公路视为直线)交通管理部门规定汽车的最高行驶速度不能超过60千米/时,并在离该公路100米处设置了一个监测点A,已知点B在A的北偏西60°方向上,点C在点A的偏东40°方向上.(1)监测发现,一辆汽车从点B匀速行驶到点C所用时间为15秒.请你通过计算,判断该越野车在这段限速路上是否超速?(参考数据:sin40°=0.64,tan40°=0.84,$\sqrt{3}$=1.73)(2)监测发现,在该路段上,一辆货车以每秒15米的速度由B处向C方向行驶,同时另一辆小汽车由C处向B方向行驶,若小汽车的速度是货车速度的$\frac{4}{3}$倍,则经过大约多少时间两车相遇(结果精确到0.01秒)
分析 (1)过点A作AD⊥BC于点D,通过解直角三角形求出BD、CD的长,再根据速度=路程÷时间即可求出越野车的速度,由此即可得出结论;
(2)先求出小汽车的速度,再根据时间=路程÷速度和,即可求出两车相遇的时间.
解答 解:(1)过点A作AD⊥BC于点D,如图所示.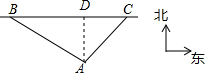
由已知得:AD=100,∠BAD=60°,∠CAD=40°,
∴BD=AD•tan∠BAD=173,CD=AD•tan∠CAD=84,
∴BC=BD+CD=257.
该越野车的速度为:257÷15×3.6=61.68(千米/时),
∵61.68>60,
∴该越野车在这段限速路上超速行驶了.
(2)小汽车的速度为:15×$\frac{4}{3}$=20(米/秒),
两车相遇的时间为:257÷(15+20)≈7.34(秒).
答:经过大约7.34秒两车相遇.
点评 本题考查了解直角三角形的应用中的方向角问题,解题的关键是:(1)求出线段BC的长度;(2)根据数量关系求出相遇时间.本题属于中档题,难度不大,解决该题型题目时,构建直角三角形通过解直角三角形求出边角是关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
12.某校为了了解240名七年级学生的体重情况,从而抽取60名学生进行测量,下列说法正确的是( )
| A. | 总体是240 | B. | 样本容量是60 | C. | 样本是60名学生 | D. | 个体是每个学生 |
4.若a>b,则下列式子中错误的是( )
| A. | a-2>b-2 | B. | a+2>b+2 | C. | $\frac{1}{2}$a>$\frac{1}{2}$b | D. | -2a>-2b |
14.下列计算中,正确的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 3$\sqrt{2}$-$\sqrt{2}$=3 | C. | $\sqrt{4\frac{1}{4}}$=2$\frac{1}{2}$ | D. | $\sqrt{(-3)^{2}}$=3 |
1.下列各组长度中,能构成直角三角形的是( )
| A. | 1,2,3 | B. | $\sqrt{2}$,$\sqrt{3}$,5 | C. | 5,6,7 | D. | 0.3,0.4,0.5 |
 如图,三角形ABC三个顶点的坐标分别为A(4,3),B(3,1),C(1,2).
如图,三角形ABC三个顶点的坐标分别为A(4,3),B(3,1),C(1,2).