题目内容
8.下列条件中,能判定四边形是平行四边形的条件是( )| A. | 一组对边平行,另一组对边相等 | B. | 一组对边平行,一组对角相等 | ||
| C. | 一组对边平行,一组邻角互补 | D. | 一组对边相等,一组邻角相等 |
分析 平行四边形的五种判定方法分别是:(1)两组对边分别平行的四边形是平行四边形;(2)两组对边分别相等的四边形是平行四边形;(3)一组对边平行且相等的四边形是平行四边形;(4)两组对角分别相等的四边形是平行四边形;(5)对角线互相平分的四边形是平行四边形.根据平行四边形的判定,逐一验证.
解答 解:A、一组对边相等,另一组对边平行,也有可能是等腰梯形;
B、一组对边平行,一组对角相等,可得到两组对角分别相等,所以是平行四边形;
C、一组对边平行,一组邻角互补,也有可能是等腰梯形;
D、一组对边相等,一组邻角相等,不一定是平行四边形.
故选:B.
点评 本题考查平行四边形的判定,注意间接条件的应用.在应用判定定理判定平行四边形时,应仔细观察题目所给的条件,仔细选择适合于题目的判定方法进行解答,避免混用判定方法.

练习册系列答案
相关题目
18.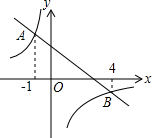 已知如图,一次函数y=ax+b和反比例函数y=$\frac{k}{x}$的图象相交于A、B两点,使不等式ax+b>$\frac{k}{x}$成立的自变量x的取值范围是( )
已知如图,一次函数y=ax+b和反比例函数y=$\frac{k}{x}$的图象相交于A、B两点,使不等式ax+b>$\frac{k}{x}$成立的自变量x的取值范围是( )
 已知如图,一次函数y=ax+b和反比例函数y=$\frac{k}{x}$的图象相交于A、B两点,使不等式ax+b>$\frac{k}{x}$成立的自变量x的取值范围是( )
已知如图,一次函数y=ax+b和反比例函数y=$\frac{k}{x}$的图象相交于A、B两点,使不等式ax+b>$\frac{k}{x}$成立的自变量x的取值范围是( )| A. | x<-1或x>4 | B. | -1<x<4 | C. | x<-1或0<x<4 | D. | -1<x<0或x>4 |
13.己知方程2xa+b-xa-b-ab=0是关于x的一元二次方程,则对应a、b的值有( )
| A. | 2组 | B. | 3组 | C. | 4组 | D. | 5组 |
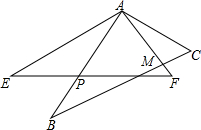 如图,在△ABC和△AEF中,∠B=∠E,AB=AE,BC=EF,∠BAE=24°,∠F=57°,边BC与AF相交于点M,边AB与EF相交于点P.
如图,在△ABC和△AEF中,∠B=∠E,AB=AE,BC=EF,∠BAE=24°,∠F=57°,边BC与AF相交于点M,边AB与EF相交于点P.