题目内容
18.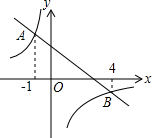 已知如图,一次函数y=ax+b和反比例函数y=$\frac{k}{x}$的图象相交于A、B两点,使不等式ax+b>$\frac{k}{x}$成立的自变量x的取值范围是( )
已知如图,一次函数y=ax+b和反比例函数y=$\frac{k}{x}$的图象相交于A、B两点,使不等式ax+b>$\frac{k}{x}$成立的自变量x的取值范围是( )| A. | x<-1或x>4 | B. | -1<x<4 | C. | x<-1或0<x<4 | D. | -1<x<0或x>4 |
分析 当一次函数的值>反比例函数的值时,直线在双曲线的上方,由此直接根据图象可以写出一次函数的值>反比例函数的值x的取值范围.
解答 解:由图象得出,一次函数y=ax+b和反比例函数y=$\frac{k}{x}$的图象的交点A、B两点的横坐标分别为-1,4,
∵等式ax+b>$\frac{k}{x}$的解集为一次函数的值>反比例函数的值x的取值范围,
∴不等式ax+b>kx的解集为x<-1或0<x<4,
故选C.
点评 本题考查一次函数的解析式y=kx+b和反比例函数y=$\frac{k}{x}$中图象问题,这里体现了数形结合的思想,做此类题一定要找到关键的点A、B.

练习册系列答案
相关题目
6.已知:a2+a+1=5,则(2+a)(1-a)的值为( )
| A. | -4 | B. | -3 | C. | -2 | D. | 7 |
13.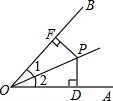 如图,∠1=∠2,PD⊥OA于D,PF⊥OB于F,下列结论错误的是( )
如图,∠1=∠2,PD⊥OA于D,PF⊥OB于F,下列结论错误的是( )
 如图,∠1=∠2,PD⊥OA于D,PF⊥OB于F,下列结论错误的是( )
如图,∠1=∠2,PD⊥OA于D,PF⊥OB于F,下列结论错误的是( )| A. | PD=PF | B. | OD=OF | C. | ∠DPO=∠FPO | D. | PD=OD |
10.下列各组单项式中,为同类项的是( )
| A. | a3与a2 | B. | -3与a | C. | 2xy与2x | D. | $\frac{1}{2}{a^2}$与2a2 |
8.下列条件中,能判定四边形是平行四边形的条件是( )
| A. | 一组对边平行,另一组对边相等 | B. | 一组对边平行,一组对角相等 | ||
| C. | 一组对边平行,一组邻角互补 | D. | 一组对边相等,一组邻角相等 |
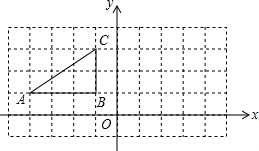 如图,方格纸中的每个小方格都是边长为1个单位的正方形.Rt△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(-4,1),点B的坐标为(-1,1).
如图,方格纸中的每个小方格都是边长为1个单位的正方形.Rt△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(-4,1),点B的坐标为(-1,1).