题目内容
20.设a,b为实数,已知关于x的方程x2-(a+b)x+$\frac{{a}^{2}+2{b}^{2}-2b+1}{2}$=0有两个实根.求a,b的取值.分析 根据方程的根的情况知△≥0,得到关于a、b的不等式,整理不等式可得a、b的值.
解答 解:∵原方程有两个实根,
∴△≥0,即[-(a+b)]2-4×$\frac{{a}^{2}+2{b}^{2}-2b+1}{2}$≥0,
整理,得:-a2-3b2+2ab+4b-2≥0,
a2-2ab+b2+2b2-4b+2≤0,
(a-b)2+2(b-1)2≤0,
∴a-b=0,b-1=0,即a=b=1.
点评 本题考查方程根的判别式,根据方程的根的情况判断△≥0是解题根本,对不等式变形得到关于a、b间关系的式子是关键.

练习册系列答案
相关题目
10.下列各组单项式中,为同类项的是( )
| A. | a3与a2 | B. | -3与a | C. | 2xy与2x | D. | $\frac{1}{2}{a^2}$与2a2 |
8.下列条件中,能判定四边形是平行四边形的条件是( )
| A. | 一组对边平行,另一组对边相等 | B. | 一组对边平行,一组对角相等 | ||
| C. | 一组对边平行,一组邻角互补 | D. | 一组对边相等,一组邻角相等 |
13.昌吉赣客运专线是我省第一条南北纵向的高速铁路,设计时速为每小时350公里,总投资约46200000000元.数字46200000000可用科学记数法表示为( )
| A. | 46.2×1010 | B. | 4.62×1011 | C. | 4.62×1010 | D. | 0.462×1011 |
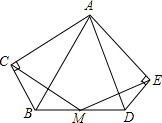 在Rt△ABC和Rt△ADE中,∠BAC=∠DAE,取BD中点M.求证:MC=ME.
在Rt△ABC和Rt△ADE中,∠BAC=∠DAE,取BD中点M.求证:MC=ME.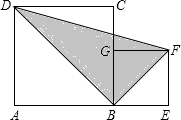 如图,正方形ABCD和正方形BEFG两正方形的面积分别是10和3,那么阴影部分面积是$\sqrt{30}$.
如图,正方形ABCD和正方形BEFG两正方形的面积分别是10和3,那么阴影部分面积是$\sqrt{30}$.