题目内容
13.己知方程2xa+b-xa-b-ab=0是关于x的一元二次方程,则对应a、b的值有( )| A. | 2组 | B. | 3组 | C. | 4组 | D. | 5组 |
分析 本题根据一元二次方程的定义,分5种情况即可.
解答 解:∵2xa+b-xa-b+ab=0是关于x的一元二次方程,
∴①$\left\{\begin{array}{l}{a+b=2}\\{a-b=1}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=\frac{3}{2}}\\{b=\frac{1}{2}}\end{array}\right.$;
②$\left\{\begin{array}{l}{a+b=2}\\{a-b=0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=1}\\{b=1}\end{array}\right.$,
③$\left\{\begin{array}{l}{a+b=1}\\{a-b=2}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=\frac{3}{2}}\\{b=-\frac{1}{2}}\end{array}\right.$;
④$\left\{\begin{array}{l}{a+b=0}\\{a-b=2}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=1}\\{b=-1}\end{array}\right.$;
⑤$\left\{\begin{array}{l}{a+b=2}\\{a-b=2}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=2}\\{b=0}\end{array}\right.$;
故选:D.
点评 本题主要考查了一元二次方程的概念.解题的关键是分5种情况讨论x的指数.

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案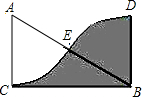 如图,△ABC中,∠C=90°,BC=$2\sqrt{3}$,若扇形ACE与扇形BDE关于点E中心对称,则图中阴影部分的面积为( )
如图,△ABC中,∠C=90°,BC=$2\sqrt{3}$,若扇形ACE与扇形BDE关于点E中心对称,则图中阴影部分的面积为( )| A. | 2 | B. | $2\sqrt{3}$ | C. | 4 | D. | $4\sqrt{3}$ |
| A. | 一组对边平行,另一组对边相等 | B. | 一组对边平行,一组对角相等 | ||
| C. | 一组对边平行,一组邻角互补 | D. | 一组对边相等,一组邻角相等 |
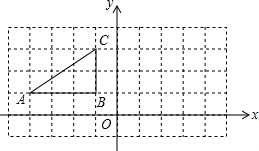 如图,方格纸中的每个小方格都是边长为1个单位的正方形.Rt△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(-4,1),点B的坐标为(-1,1).
如图,方格纸中的每个小方格都是边长为1个单位的正方形.Rt△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(-4,1),点B的坐标为(-1,1).