题目内容
7. 已知,如图,AD,BE,CF是△ABC的三条中线,四边形BFCH是平行四边形,求证:AD∥EH.
已知,如图,AD,BE,CF是△ABC的三条中线,四边形BFCH是平行四边形,求证:AD∥EH.
分析 由四边形BFCH是平行四边形,故D为对角线的中点,是平行四边形的中心,FH必过点D,且FD=HD,AF=BF,BD=CD,根据三角形中位线定理,证得DF∥AC,FD=$\frac{1}{2}$AC=AE,证得四边形ADHE是平行四边形,即可证得结论.
解答  证明:连接FH,
证明:连接FH,
∵四边形BFCH是平行四边形,BC是对角线,
∴D为对角线的中点,是平行四边形的中心,
∴FH必过点D,且FD=HD,AF=BF,BD=CD,
DF是△BAC的中位线,
∴DF∥AC,FD=$\frac{1}{2}$AC=AE,
即:HD∥AE,HD=AE,
∴四边形ADHE是平行四边形,
∴AD∥EH.
点评 本题主要考查了平行四边形的判定和性质,三角形中位线定理,正确作出辅助线,证得FH必过D点是解题的关键.

练习册系列答案
相关题目
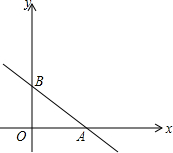 如图,直线y=-$\frac{3}{4}$x+3交坐标轴于A,B两点,将线段AB绕点A顺时针旋转90°,得到线段AC,连接BC.
如图,直线y=-$\frac{3}{4}$x+3交坐标轴于A,B两点,将线段AB绕点A顺时针旋转90°,得到线段AC,连接BC.
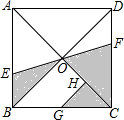 如图,在正方形ABCD中,对角线AC,BD相交于点O,过点O作线段EF,分别交AB,CD于点E,F,过BC中点G作GH∥BD,交AC于点H,已知正方形的边长为4cm,求图中阴影部分的面积.
如图,在正方形ABCD中,对角线AC,BD相交于点O,过点O作线段EF,分别交AB,CD于点E,F,过BC中点G作GH∥BD,交AC于点H,已知正方形的边长为4cm,求图中阴影部分的面积. 小明和小华沿同一路线从学校出发到图书馆查阅资料,学校与图书馆的路程是3km,小明骑自行车小华步行,两人离出发地的路程S(km)和经过的时间t(min)之间的函数关系的图象如图所示,根据图中的信息可知小明与小华迎面相遇时,他们离学校的路程是2.25km.
小明和小华沿同一路线从学校出发到图书馆查阅资料,学校与图书馆的路程是3km,小明骑自行车小华步行,两人离出发地的路程S(km)和经过的时间t(min)之间的函数关系的图象如图所示,根据图中的信息可知小明与小华迎面相遇时,他们离学校的路程是2.25km.