题目内容

2．若关于x的不等式组$\left\{\begin{array}{l}{x＜a-2}\\{x+1＞0}\end{array}\right.$只有4个整数解，则a的取值范围是5＜a≤6．

分析 首先求出不等式的解集，根据不等式组整数解的个数就可以确定有哪些整数解，根据解的情况可以得到关于a的不等式，从而求出a的范围．

解答 解：解不等式x+1＞0，得：x＞-1，
∵不等式组只有4个整数解，
∴3＜a-2≤4，
解得：5＜a≤6，
故答案为：5＜a≤6．

点评 考查不等式组的解法及整数解的确定．求不等式组的解集，应遵循以下原则：同大取较大，同小取较小，小大大小中间找，大大小小解不了．

练习册系列答案
相关题目
12．（1）（$\frac{1}{4}$）-1-$\sqrt{27}$+（5-π）0+6tan60°．
（2）如果k是数据-3，5，-1，-2，8中的中位数，求关于x的方程$\frac{1-x}{x-2}$+$\frac{k}{2-x}$=1的解．
13．$\sqrt{2x-3}$在实数范围内有意义，则x的取值范围是（　　）
A．x≥$\frac{3}{2}$B．x＞$\frac{3}{2}$C．x≤$\frac{3}{2}$D．x＜$\frac{3}{2}$
10．2015年某企业有4000名职工，为了了解职工本年度第一个季度网上购物的情况，该企业从中随机抽取了350名职工，按年龄分布和对网上购物情况进行了调查统计，并将统计结果绘成了频数分布直方图（每个组距包含左边的数，但不包含右边的数）和扇形统计图．
（1）这次调查中，如果被调查职工年龄的中位数是整数，那么这个中位数所在的年龄段是哪一段？
（2）你估计这个企业的4000名职工中，从不网购的有多少人？
（3）统计显示，买同样的商品，经常网购的人比在一般商店购买能节省20%，偶尔网购的人比在一般商店购买能节省15%，样本中，职工第一季度网购商品共消费24500元，这些商品若在一般商店购买需要30000元，请问，经常网购的一组和偶尔网购的一组本季度网购商品各消费多少元？
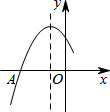17．如图是二次函数y=ax2+bx+c图象的一部分，图象过点A（-3，0），对称轴为直线x=-1，给出四个结论：
①b2＞4ac；
②2a+b=0；
③a+b+c＞0；
④若点B（-$\frac{5}{2}$，y1），C（-$\frac{1}{2}$，y2）为函数图象上的两点，则y1＜y2．
其中正确结论是①④．
7．已知，如图，AD，BE，CF是△ABC的三条中线，四边形BFCH是平行四边形，求证：AD∥EH．
14．计算：$\frac{2}{a-1}$-$\frac{2a}{a-1}$=-2．
11．（1）计算：（-1）2016+（$\frac{1}{3}$）-1+|-$\sqrt{2}$|-2sin45°．
（2）解不等式x-1≤$\frac{2x-1}{3}$，并写出不等式的正整数解．
5．计算：5（6+1）（62+1）（64+1）+1，结果为（　　）
A．616B．68C．68+1D．68-1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网