题目内容
10. 小明和小华沿同一路线从学校出发到图书馆查阅资料,学校与图书馆的路程是3km,小明骑自行车小华步行,两人离出发地的路程S(km)和经过的时间t(min)之间的函数关系的图象如图所示,根据图中的信息可知小明与小华迎面相遇时,他们离学校的路程是2.25km.
小明和小华沿同一路线从学校出发到图书馆查阅资料,学校与图书馆的路程是3km,小明骑自行车小华步行,两人离出发地的路程S(km)和经过的时间t(min)之间的函数关系的图象如图所示,根据图中的信息可知小明与小华迎面相遇时,他们离学校的路程是2.25km.
分析 根据待定系数法分别求出直线OD、直线BC的解析式,列出方程组求出OD与BC交点坐标即可得答案.
解答 解:设直线OD的解析式为:S=kt,
将点D(30,3)代入,得:30k=3,
解得:k=0.1,
∴直线OD的解析式为:S=0.1t,
设直线BC的解析式为:S=mt+n,
将点B(20,3)、点C(30,0)代入,得:
$\left\{\begin{array}{l}{20m+n=3}\\{30m+n=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=-0.3}\\{n=9}\end{array}\right.$,
∴直线BC的解析式为:S=-0.3t+9,
根据题意,得:$\left\{\begin{array}{l}{S=0.1t}\\{S=-0.3t+9}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{t=22.5}\\{S=2.25}\end{array}\right.$,
即当t=22.5min时,小明与小华迎面相遇,此时距离学校2.25km,
故答案为:2.25.
点评 本题主要考查一次函数的实际应用能力,从图象中获得所需的信息是需要掌握的基本能力,还要会熟练地运用待定系数法求函数解析式和使用方程组求交点坐标的方法.

练习册系列答案
相关题目
8.某次捐款活动中,7位同学的捐款金额分别是5元,6元,6元,7元,8元,9元,10元,则这组数据的中位数与众数分别是( )
| A. | 6,6 | B. | 7,6 | C. | 7,8 | D. | 6,8 |
5.计算:5(6+1)(62+1)(64+1)+1,结果为( )
| A. | 616 | B. | 68 | C. | 68+1 | D. | 68-1 |
20.$\frac{1}{2}$sin60°的值等于( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{4}$ | D. | $\sqrt{3}$ |
 已知,如图,AD,BE,CF是△ABC的三条中线,四边形BFCH是平行四边形,求证:AD∥EH.
已知,如图,AD,BE,CF是△ABC的三条中线,四边形BFCH是平行四边形,求证:AD∥EH.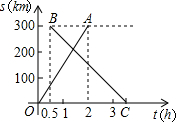 在甲、乙两城市之间每隔1小时有一列速度相同的动车组列车从甲城开往乙城.如图所示,OA是第一列动车组列车离开甲城的路程s(千米)与运行时间t(时)的函数图象,BC是一列从乙城开往甲城的普通快车距甲城的路程s(千米)与运行时间t(时)的函数图象.请根据图中信息,解答下列问题:
在甲、乙两城市之间每隔1小时有一列速度相同的动车组列车从甲城开往乙城.如图所示,OA是第一列动车组列车离开甲城的路程s(千米)与运行时间t(时)的函数图象,BC是一列从乙城开往甲城的普通快车距甲城的路程s(千米)与运行时间t(时)的函数图象.请根据图中信息,解答下列问题: 如图所示,在△ABC中,∠CAB=70°,在同一平面内,将△ABC绕A点逆时针旋转到△AB′C′的位置,使CC′∥AB,则∠BAB′=40°.
如图所示,在△ABC中,∠CAB=70°,在同一平面内,将△ABC绕A点逆时针旋转到△AB′C′的位置,使CC′∥AB,则∠BAB′=40°.