题目内容
12.已知关于x的一元二次方程x2+4x+m-1=0有两个不相等的实数根.(1)求m的取值范围;
(2)设x1、x2方程的两个实数根,请你为m选取一个合适的整数,求x${\;}_{1}^{2}$+x${\;}_{2}^{2}$+x1x2的值.
分析 (1)根据判别式的意义得到△=42-4(m-1)>0,然后解不等式即可;
(2)在(1)的范围内取m=1,则根据根与系数的关系得到x1+x2=-4,x1x2=0,再把x${\;}_{1}^{2}$+x${\;}_{2}^{2}$+x1x2变形为(x1+x2)2-x1x2,然后利用整体代入的方法计算.
解答 解:(1)根据题意得△=42-4(m-1)>0,
解得m<5;
(2)当m=1时,方程化为x2+4x=0,
则x1+x2=-4,x1x2=0,
所以x${\;}_{1}^{2}$+x${\;}_{2}^{2}$+x1x2=(x1+x2)2-x1x2=(-4)2-0=16.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.也考查了根的判别式.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
3.近年来,某市水产养殖得到迅猛发展,水产养殖业已成为沿海某些城镇的支柱产业之一,某养殖场2014年养殖了20亩紫菜,平均每亩紫菜的常量为300kg,根据市场需要,2015年该养殖扩大养殖面积.并且全部养殖高产的新品种,已知紫菜养殖面积的增长率是平均每亩产量增长率的2倍,2015年紫菜的总产量为18000kg,设紫菜平均每亩产量的增长率为x.
(1)完成下表(用含x的代数式表示2015年的平均每亩产量和养殖面积):
(2)求紫菜平均每亩产量的增长率x.
(1)完成下表(用含x的代数式表示2015年的平均每亩产量和养殖面积):
| 年份 品种 | 2014年 | 2015年 |
| 平均每亩产量(kg) | 300 | 300(1+x) |
| 养殖面积(亩) | 20 | 20(1+2x) |
17.某班体育委员记录了第一小组七位同学定点投篮(每人投10个)的情况,投进篮框的个数为6,10,5,3,4,8,4,这组数据的众数和极差分别是( )
| A. | 5,7 | B. | 7,5 | C. | 4,7 | D. | 3,7 |
1.绝对值最小的有理数是( )
| A. | -1 | B. | 0 | C. | 1 | D. | 不存在 |
 如图,A(-4,0),B(0,2),C(0,4).点D为x轴上一点,CD交直线AB于P,若△AOB≌△COD,求点P的坐标.
如图,A(-4,0),B(0,2),C(0,4).点D为x轴上一点,CD交直线AB于P,若△AOB≌△COD,求点P的坐标. 已知,如图,AD,BE,CF是△ABC的三条中线,四边形BFCH是平行四边形,求证:AD∥EH.
已知,如图,AD,BE,CF是△ABC的三条中线,四边形BFCH是平行四边形,求证:AD∥EH.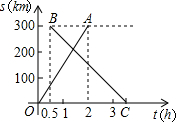 在甲、乙两城市之间每隔1小时有一列速度相同的动车组列车从甲城开往乙城.如图所示,OA是第一列动车组列车离开甲城的路程s(千米)与运行时间t(时)的函数图象,BC是一列从乙城开往甲城的普通快车距甲城的路程s(千米)与运行时间t(时)的函数图象.请根据图中信息,解答下列问题:
在甲、乙两城市之间每隔1小时有一列速度相同的动车组列车从甲城开往乙城.如图所示,OA是第一列动车组列车离开甲城的路程s(千米)与运行时间t(时)的函数图象,BC是一列从乙城开往甲城的普通快车距甲城的路程s(千米)与运行时间t(时)的函数图象.请根据图中信息,解答下列问题: