题目内容
17.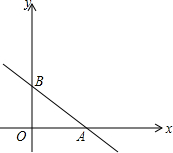 如图,直线y=-$\frac{3}{4}$x+3交坐标轴于A,B两点,将线段AB绕点A顺时针旋转90°,得到线段AC,连接BC.
如图,直线y=-$\frac{3}{4}$x+3交坐标轴于A,B两点,将线段AB绕点A顺时针旋转90°,得到线段AC,连接BC.①补全图形,并直接写出点C的坐标:(7,4);
②点D是直线y=x上的一个点,且满足S△ABD=S△ABC,求出点D的坐标.
分析 (1)先根据坐标轴上点的坐标特征求出B点坐标为(0,3),A点坐标为(4,0),则OA=4,OB=3,根据全等三角形的性质即可得到结论;
(2)由点D是直线y=x上的一个点,设D(m,m),根据S△ABD=S△ABC,得到CD∥AB,求得直线CD的解析式为y=-$\frac{3}{4}$x+$\frac{37}{4}$,即可得到结论.
解答 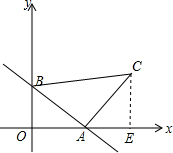 解:(1)如图,当x=0时,y=-$\frac{3}{4}$x+3=3,则B点坐标为(0,3);
解:(1)如图,当x=0时,y=-$\frac{3}{4}$x+3=3,则B点坐标为(0,3);
当y=0时,-$\frac{3}{4}$x+3=0,解得x=4,则A点坐标为(4,0),
则OA=4,OB=3,
∴AB=5,
∵将线段AB绕点A顺时针旋转90°,得到线段AC,
∴∠BAC=90°,AB=AC=5,
过C作CE⊥x轴于E,
∴∠ADC=∠AOB=90°,
在△AOB与△AEC中,
$\left\{\begin{array}{l}{∠AEC=∠AOB}\\{∠ABC=∠EAC}\\{AC=AB}\end{array}\right.$,
∴△AOB≌△AEC,
∴CE=OA=4,AE=OB=3,
∴C(7,4);
故答案为:(7,4);
(2)∵点D是直线y=x上的一个点,
设D(m,m),
∵S△ABD=S△ABC,
∴CD∥AB,
设直线CD的解析式为y=-$\frac{3}{4}$x+b,
∴-$\frac{3}{4}$×7+b=4,
∴b=$\frac{37}{4}$,
∴直线CD的解析式为y=-$\frac{3}{4}$x+$\frac{37}{4}$,
∴m=-$\frac{3}{4}$m+$\frac{37}{4}$,
∴m=$\frac{37}{7}$,
∴D($\frac{37}{7}$,$\frac{37}{7}$).
点评 本题考查了一次函数图形上点的坐标特征,坐标与图形的变换-旋转,待定系数法求函数的解析式,熟练掌握待定系数法求函数的解析式是解题的关键.

| A. | m>y1>y2 | B. | m>y2>y1 | C. | y1>y2>m | D. | y2>y1>m |
 如图,A(-4,0),B(0,2),C(0,4).点D为x轴上一点,CD交直线AB于P,若△AOB≌△COD,求点P的坐标.
如图,A(-4,0),B(0,2),C(0,4).点D为x轴上一点,CD交直线AB于P,若△AOB≌△COD,求点P的坐标.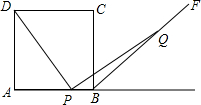 如图,正方形ABCD中,P为边AB上一动点,BF是∠ABC的外角平分线,Q是BF上一点,且PQ=DP,那么DP与PQ是否一定满足垂直关系?说明理由.
如图,正方形ABCD中,P为边AB上一动点,BF是∠ABC的外角平分线,Q是BF上一点,且PQ=DP,那么DP与PQ是否一定满足垂直关系?说明理由. 已知,如图,AD,BE,CF是△ABC的三条中线,四边形BFCH是平行四边形,求证:AD∥EH.
已知,如图,AD,BE,CF是△ABC的三条中线,四边形BFCH是平行四边形,求证:AD∥EH.