题目内容
9.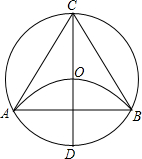 如图所示,CD是⊙O的直径,以点D为圆心,DO长为半径作弧交⊙O于点A,B,求证:△ABC为等边三角形.
如图所示,CD是⊙O的直径,以点D为圆心,DO长为半径作弧交⊙O于点A,B,求证:△ABC为等边三角形.
分析 连接AO、AD、BO、BD,根据等边三角形的判定证得△AOD和△BOD是等边三角形,根据菱形的判定定理得到四边形ADBO是菱形,根据菱形的性质和圆周角定理证明结论.
解答 证明: 连接AO、AD、BO、BD,
连接AO、AD、BO、BD,
由题意得,OB=OA=BD=AD=OD,
∴△AOD和△BOD是等边三角形,即四边形ADBO是菱形,
∴∠AOB=120°,
∴∠ACB=60°,
∵四边形ADBO是菱形,
∴CD垂直平分AB,
∴CA=CB,又∠ACB=60°,
∴△ABC为等边三角形.
点评 本题考查了圆心角、弧、弦的关系,等边三角形的判定和性质,菱形的判定和性质,作出辅助线构建等边三角形是解题的关键.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
20.缸内红茶菌的面积每天长大一倍,若16天长满整个缸面,那么经过( )天长满缸面的一半.
| A. | 8 | B. | 9 | C. | 16 | D. | 15 |
17.抛物线y=2(x+3)2-4的顶点坐标是( )
| A. | (3,4) | B. | (-3,4) | C. | (-3,-4) | D. | (3,-4) |
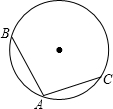 如图.⊙O的半径为2$\sqrt{2}$,AB、AC是⊙O的两条弦,AB=2$\sqrt{3}$,AC=4,如果以O为圆心,作一个与直线AC相切的圆,那么:
如图.⊙O的半径为2$\sqrt{2}$,AB、AC是⊙O的两条弦,AB=2$\sqrt{3}$,AC=4,如果以O为圆心,作一个与直线AC相切的圆,那么: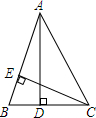 如图,在△ABC中,AD,CE是△ABC的高,找出图中的一组比例线段,并说明理由.
如图,在△ABC中,AD,CE是△ABC的高,找出图中的一组比例线段,并说明理由.