题目内容
14.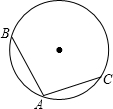 如图.⊙O的半径为2$\sqrt{2}$,AB、AC是⊙O的两条弦,AB=2$\sqrt{3}$,AC=4,如果以O为圆心,作一个与直线AC相切的圆,那么:
如图.⊙O的半径为2$\sqrt{2}$,AB、AC是⊙O的两条弦,AB=2$\sqrt{3}$,AC=4,如果以O为圆心,作一个与直线AC相切的圆,那么:(1)所作的圆的半径是多少?
(2)所作的圆与直线AB有怎样的位置关系?为什么?
分析 (1)作OE⊥AC于E,连接OA,根据垂径定理和勾股定理求出OE的长,根据直线与圆的位置关系得到答案;
(2)求出OF的长,根据直线与圆的位置关系进行判定.
解答 解:(1)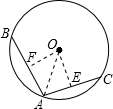 作OE⊥AC于E,连接OA,
作OE⊥AC于E,连接OA,
则AE=$\frac{1}{2}$AC=2,
则OE=$\sqrt{O{A}^{2}-A{E}^{2}}$=2,
答:以O为圆心,作一个与直线AC相切的圆,所作的圆的半径是2;
(2)作OF⊥AB于F,
则AF=$\frac{1}{2}$AB=$\sqrt{3}$,
∴OF=$\sqrt{O{A}^{2}-A{F}^{2}}$=$\sqrt{5}$,
∵$\sqrt{5}$>2,
∴所作的圆与直线AB相离.
点评 本题考查的是直线与圆的位置关系,如果圆心到直线的距离为d,圆的半径为r,若d<r,则直线与圆相交;若d=r,则直线于圆相切;若d>r,则直线与圆相离.

练习册系列答案
相关题目
6.下列命题中,正确的是( )
| A. | 所有的直角三角形都相似 | |
| B. | 所有矩形都相似 | |
| C. | 有一个角为30°的两个等腰三角形相似 | |
| D. | 所有等边三角形都相似 |
 把-1.5,-2,2,π各数(或近似值)在数轴上表示出来,并比较它们的大小,用“<”号连接.
把-1.5,-2,2,π各数(或近似值)在数轴上表示出来,并比较它们的大小,用“<”号连接.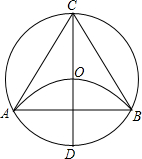 如图所示,CD是⊙O的直径,以点D为圆心,DO长为半径作弧交⊙O于点A,B,求证:△ABC为等边三角形.
如图所示,CD是⊙O的直径,以点D为圆心,DO长为半径作弧交⊙O于点A,B,求证:△ABC为等边三角形. 如图,点P在线段AB上,且$\frac{AP}{AB}$=$\frac{PB}{AP}$,若AB=10cm,求AP的长.
如图,点P在线段AB上,且$\frac{AP}{AB}$=$\frac{PB}{AP}$,若AB=10cm,求AP的长.