题目内容
已知关于x的方程(m+1)x2+2mx-3=0
(1)有两个实数根,则m的取值范围为 ;
(2)若只有一个根,则m的取值范围为 .
(1)有两个实数根,则m的取值范围为
(2)若只有一个根,则m的取值范围为
考点:根的判别式,一元一次方程的解
专题:计算题
分析:(1)根据一元二次方程的定义和判别式的意义得到m+1≠0且△=4m2-4(m+1)×(-3)≥0,其中4m2-4(m+1)×(-3)≥0的解集为全体实数,则m的范围为m≠-1;
(2)根据一元一次方程的解得到m+1=0,然后解关于m的方程.
(2)根据一元一次方程的解得到m+1=0,然后解关于m的方程.
解答:解:(1)根据题意得m+1≠0且△=4m2-4(m+1)×(-3)≥0,
解得m≠-1;
(2)根据题意得m+1=0,解得m=-1.
故答案为m≠-1,m=-1.
解得m≠-1;
(2)根据题意得m+1=0,解得m=-1.
故答案为m≠-1,m=-1.
点评:本题考查了利用一元二次方程根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
不等式x+5≥3x的正整数解有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
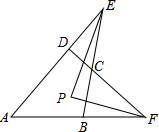 四边形ABCD中,AD、BC的延长线交于E,AB、DC的延长线交于F,∠AEB、∠AFD的平分线交于点P,∠A=44°,∠BCD=136°.
四边形ABCD中,AD、BC的延长线交于E,AB、DC的延长线交于F,∠AEB、∠AFD的平分线交于点P,∠A=44°,∠BCD=136°.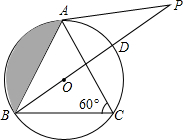 如图,在△ABC中,∠C=60°,⊙O是△ABC的外接圆,点P在直径BD的延长线上,且AB=AP.
如图,在△ABC中,∠C=60°,⊙O是△ABC的外接圆,点P在直径BD的延长线上,且AB=AP.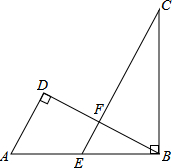 如图,在△ABD中,∠D=90°,点E是AB中点,BC⊥AB,且EC∥AD交BD于点F,若AB=4,BC=2
如图,在△ABD中,∠D=90°,点E是AB中点,BC⊥AB,且EC∥AD交BD于点F,若AB=4,BC=2