题目内容
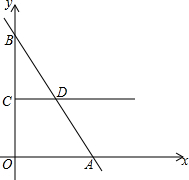 如图,在平面直角坐标系中,直线l:y=kx+20与x轴、y轴分别交于点A、B,OB=2AO,过点C(0,8)做射线CD交直线l于点D,且CD∥x轴.动点P从点O出发沿y轴的正半轴向点B运动,速度为每秒2个单位长度.过点P做x轴的平行线交直线l于点Q.
如图,在平面直角坐标系中,直线l:y=kx+20与x轴、y轴分别交于点A、B,OB=2AO,过点C(0,8)做射线CD交直线l于点D,且CD∥x轴.动点P从点O出发沿y轴的正半轴向点B运动,速度为每秒2个单位长度.过点P做x轴的平行线交直线l于点Q.(1)设点P的运动时间为t(秒),求△PAQ的面积S关于t的函数关系式;
(2)将Rt△OPA沿直线PA折叠得到Rt△O′PA.是否存在t值,使Rt△O′PA的顶点O′恰好落在射线CD上?若存在求出t的值,若不存在,请说明理由.
考点:一次函数综合题
专题:
分析:(1)根据待定系数法,可得AB的解析式,根据P点移动的速度与移动时间,可得OP的长,根据函数值,可得相应自变量的值,即PQ的长,根据三角形的面积公式,可得答案;
(2)根据轴对称的性质,可得OA=O′A,OP=O′P,根据解方程组,可得答案.
(2)根据轴对称的性质,可得OA=O′A,OP=O′P,根据解方程组,可得答案.
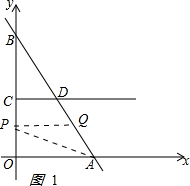
解答:解:(1)如图1:
 ,
,
由y=x+20,当x=0时,得OB=20,
由OB2=OA,得OA=10,即A(10,0).
把(10,0)代入y=kx+20,得10k+20=0.
解得k=-2,
直线l的解析式为 y=-2x+20.
由动点P从点O出发沿y轴的正半轴向点B运动,速度为每秒2个单位长度,得OP=2t,即P(0,2t).
由过点P做x轴的平行线交直线l于点Q,得-2x+20=2t,解得x=10-t,即Q(10-t,2t).
S△PAQ=
PQ•PO=
(10-t)2t=-t2+10t,
即△PAQ的面积S关于t的函数关系式S=-t2-10t;
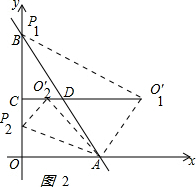
(2)存在t值,Rt△O′PA的顶点O′恰好落在射线CD上,如图2:
 ,
,
设O′点的坐标为(a,8),P点坐标是(0,2t),
由Rt△OPA沿直线PA折叠得到Rt△O′PA,得
,即
,
解①得a=16,或a=4,
当a=16时,②化简,得32t=16×16+64,解得t=10,
当a=4时,32t=80,解得t=
.
综上所述:t=
或t=10时,Rt△O′PA的顶点O′恰好落在射线CD上.
 ,
,由y=x+20,当x=0时,得OB=20,
由OB2=OA,得OA=10,即A(10,0).
把(10,0)代入y=kx+20,得10k+20=0.
解得k=-2,
直线l的解析式为 y=-2x+20.
由动点P从点O出发沿y轴的正半轴向点B运动,速度为每秒2个单位长度,得OP=2t,即P(0,2t).
由过点P做x轴的平行线交直线l于点Q,得-2x+20=2t,解得x=10-t,即Q(10-t,2t).
S△PAQ=
| 1 |
| 2 |
| 1 |
| 2 |
即△PAQ的面积S关于t的函数关系式S=-t2-10t;
(2)存在t值,Rt△O′PA的顶点O′恰好落在射线CD上,如图2:
 ,
,设O′点的坐标为(a,8),P点坐标是(0,2t),
由Rt△OPA沿直线PA折叠得到Rt△O′PA,得
|
|
解①得a=16,或a=4,
当a=16时,②化简,得32t=16×16+64,解得t=10,
当a=4时,32t=80,解得t=
| 5 |
| 2 |
综上所述:t=
| 5 |
| 2 |
点评:本题考查了一次函数综合题,利用了待定系数求函数解析式,利用函数值得出相应自变量的值,三角形的面积公式;(2)利用了轴对称的性质得出方程组是解题关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
已知等腰三角形的一个外角等于110°,则它的顶角度数是( )度.
| A、40 | B、70 |
| C、40或70 | D、140 |
不等式x+5≥3x的正整数解有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
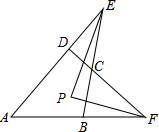 四边形ABCD中,AD、BC的延长线交于E,AB、DC的延长线交于F,∠AEB、∠AFD的平分线交于点P,∠A=44°,∠BCD=136°.
四边形ABCD中,AD、BC的延长线交于E,AB、DC的延长线交于F,∠AEB、∠AFD的平分线交于点P,∠A=44°,∠BCD=136°.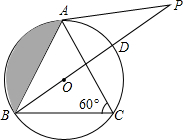 如图,在△ABC中,∠C=60°,⊙O是△ABC的外接圆,点P在直径BD的延长线上,且AB=AP.
如图,在△ABC中,∠C=60°,⊙O是△ABC的外接圆,点P在直径BD的延长线上,且AB=AP.