题目内容
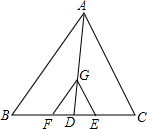 如图,在△ABC中,AD是中线,G是AD上一点,AG=2GD,CF∥AB,CE∥AC,分别交BC于点F、E.
如图,在△ABC中,AD是中线,G是AD上一点,AG=2GD,CF∥AB,CE∥AC,分别交BC于点F、E.(1)若△GFE的周长为5.5,求△ABC的周长;
(2)若BC=6,△ABC的边BC上的高为5,求△GFE的面积.
考点:相似三角形的判定与性质,三角形的重心
专题:
分析:(1)易证△ABC∽△GFE,由相似三角形的性质:周长之比等于相似比即可求出△ABC的周长;
(2)由(1)可知△ABC∽△GFE,由相似三角形的性质:面积之比等于相似比的平方即可求出△GFE的面积.
(2)由(1)可知△ABC∽△GFE,由相似三角形的性质:面积之比等于相似比的平方即可求出△GFE的面积.
解答:解:(1)∵GE∥AC,
∴∠C=∠GEF,
∵CF∥AB,
∴∠B=∠GFE,
∴△ABC∽△GFE,
∵AG=2GD,
∴GD:AD=GF;AB=1:3,
∴△ABC周长为5.5×3=16.5;
(2)∵△ABC∽△GFE,
∴
=9,
S△ABC=
×5×6=15,
∴S△GEF=
S△ABC=
=
.
∴∠C=∠GEF,
∵CF∥AB,
∴∠B=∠GFE,
∴△ABC∽△GFE,
∵AG=2GD,
∴GD:AD=GF;AB=1:3,
∴△ABC周长为5.5×3=16.5;
(2)∵△ABC∽△GFE,
∴
| S△ABC |
| S△GEF |
S△ABC=
| 1 |
| 2 |
∴S△GEF=
| 1 |
| 9 |
| 15 |
| 9 |
| 5 |
| 3 |
点评:本题考查了相似三角形的判定和性质,解题的关键是熟记各种判定三角形相似的方法和各种相似的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
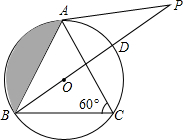 如图,在△ABC中,∠C=60°,⊙O是△ABC的外接圆,点P在直径BD的延长线上,且AB=AP.
如图,在△ABC中,∠C=60°,⊙O是△ABC的外接圆,点P在直径BD的延长线上,且AB=AP. 如图,AB∥CD,直线MN与AB、CD分别交于点E、F,∠AEM=2∠MEB,求∠DFN的度数.
如图,AB∥CD,直线MN与AB、CD分别交于点E、F,∠AEM=2∠MEB,求∠DFN的度数.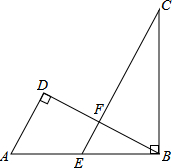 如图,在△ABD中,∠D=90°,点E是AB中点,BC⊥AB,且EC∥AD交BD于点F,若AB=4,BC=2
如图,在△ABD中,∠D=90°,点E是AB中点,BC⊥AB,且EC∥AD交BD于点F,若AB=4,BC=2 如图,已知△ABC中,CE⊥AB于E,BF⊥AC于F,在不添加字母的情况下,找出图中所有的相似三角形,并证明其中一组.
如图,已知△ABC中,CE⊥AB于E,BF⊥AC于F,在不添加字母的情况下,找出图中所有的相似三角形,并证明其中一组.