题目内容
5.已知:一个正数的两个平方根分别是2a-2和a-4,则这个正数的立方根是$\root{3}{4}$.分析 根据一个正数的平方根有2个,且互为相反数求出a的值,即可确定出正数的立方根.
解答 解:根据题意得:2a-2+a-4=0,
解得:a=2,
∴这个正数为(2×2-2)2=4,
则这个正数的立方根是$\root{3}{4}$,
故答案为:$\root{3}{4}$
点评 此题考查了立方根,以及平方根,熟练掌握各自的定义是解本题的关键.

练习册系列答案
相关题目
16.从1-9这九个自然数中任取一个,是2的倍数的概率是( )
| A. | $\frac{2}{3}$ | B. | $\frac{5}{9}$ | C. | $\frac{4}{9}$ | D. | $\frac{2}{9}$ |
13.若代数式x2-6x+b可化为(x-a)2-1,则b+a的值( )
| A. | 3 | B. | 4 | C. | 11 | D. | 6 |
20.下列各式中是二元一次方程的是( )
| A. | x+π=4 | B. | 2x-y | C. | 3x+y=0 | D. | 2x-5=y2 |
10.若α,β是方程x2-2x-2=0的两个实数根,则α2+β2的值为( )
| A. | 10 | B. | 9 | C. | 8 | D. | 7 |
17.在数学课上,同学们都判断出命题“若m<n,则m2<${n}^{{2}^{m}}$”是假命题,下列是四位同学举出的反例,其中不正确的是( )
| A. | m=-1,n=2 | B. | m=-5,n=2 | C. | m=-4,n=-2 | D. | m=-8,n=-2 |
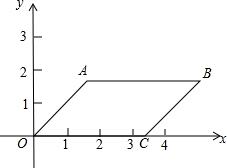 如图,在平行四边形OABC中,已知AB=OC,AB∥OC.A、C两点的坐标分别为$A(\sqrt{3},\sqrt{3}),C(2\sqrt{3},0)$.
如图,在平行四边形OABC中,已知AB=OC,AB∥OC.A、C两点的坐标分别为$A(\sqrt{3},\sqrt{3}),C(2\sqrt{3},0)$. 如图,在△ABC中,AB=AC,∠BAC=90°,点D是BC上一点,DE∥AB,AE∥BC,DE分别交AC、AE于点O和E,连接AD、CE.
如图,在△ABC中,AB=AC,∠BAC=90°,点D是BC上一点,DE∥AB,AE∥BC,DE分别交AC、AE于点O和E,连接AD、CE. 小明将一块三角形的玻璃棒摔碎成如图所示的四块(即图中标有1,2,3,4的四块),若只带一块配成原来一样大小的三角形,则应该带第2块.
小明将一块三角形的玻璃棒摔碎成如图所示的四块(即图中标有1,2,3,4的四块),若只带一块配成原来一样大小的三角形,则应该带第2块.