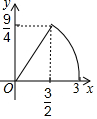题目内容
15.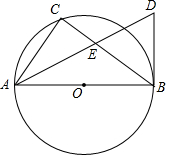 如图,AB是⊙O直径,点C在⊙O上,AD平分∠CAB,BD是⊙O的切线,AD与BC相交于点E.
如图,AB是⊙O直径,点C在⊙O上,AD平分∠CAB,BD是⊙O的切线,AD与BC相交于点E.(1)求证:BD=BE;
(2)若DE=2,BD=$\sqrt{5}$,求CE的长.
分析 (1))设∠BAD=α,由于AD平分∠BAC,所以∠CAD=∠BAD=α,进而求出∠D=∠BED=90°-α,从而可知BD=BE;
(2)设CE=x,由于AB是⊙O的直径,∠AFB=90°,又因为BD=BE,DE=2,FE=FD=1,由于BD=$\sqrt{5}$,所以tanα=$\frac{1}{2}$,从而可求出AB=$\frac{BF}{sinα}$=2$\sqrt{5}$,利用勾股定理列出方程即可求出x的值.
解答 解:(1)设∠BAD=α,
∵AD平分∠BAC
∴∠CAD=∠BAD=α,
∵AB是⊙O的直径,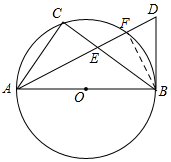 ∴∠ACB=90°,
∴∠ACB=90°,
∴∠ABC=90°-2α,
∵BD是⊙O的切线,
∴BD⊥AB,
∴∠DBE=2α,
∠BED=∠BAD+∠ABC=90°-α,
∴∠D=180°-∠DBE-∠BED=90°-α,
∴∠D=∠BED,
∴BD=BE
(2)设AD交⊙O于点F,CE=x,连接BF,
∵AB是⊙O的直径,
∴∠AFB=90°,
∵BD=BE,DE=2,
∴FE=FD=1,
∵BD=$\sqrt{5}$,
∴tanα=$\frac{1}{2}$,
∴AC=2x
∴AB=$\frac{BF}{sinα}$=2$\sqrt{5}$
在Rt△ABC中,
由勾股定理可知:(2x)2+(x+$\sqrt{5}$)2=(2$\sqrt{5}$)2,
∴解得:x=-$\sqrt{5}$或x=$\frac{3\sqrt{5}}{5}$,
∴CE=$\frac{3\sqrt{5}}{5}$;
点评 本题考查圆的综合问题,涉及切线的性质,圆周角定理,勾股定理,解方程等知识,综合程度较高,属于中等题型.

练习册系列答案
相关题目
7.下列运算正确的是( )
| A. | 3a+2a=5a2 | B. | 3a+3b=3ab | C. | 2a2bc-a2bc=a2bc | D. | a5-a2=a3 |
5.化简:$\frac{x}{x-y}$-$\frac{y}{x+y}$,结果正确的是( )
| A. | 1 | B. | $\frac{{x}^{2}+{y}^{2}}{{x}^{2}-{y}^{2}}$ | C. | $\frac{x-y}{x+y}$ | D. | x2+y2 |
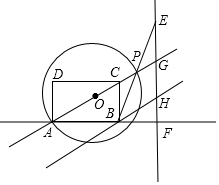 如图,在矩形ABCD中,∠CAB=30°,P是直线AC上一动点,连结BP并延长至点E,使BP=PE,过点E作EF⊥AB于点F,交直线AC于点G,过点B作BH∥AC交直线EF于点H,以AP为直径的⊙O交直线AB于点Q.
如图,在矩形ABCD中,∠CAB=30°,P是直线AC上一动点,连结BP并延长至点E,使BP=PE,过点E作EF⊥AB于点F,交直线AC于点G,过点B作BH∥AC交直线EF于点H,以AP为直径的⊙O交直线AB于点Q.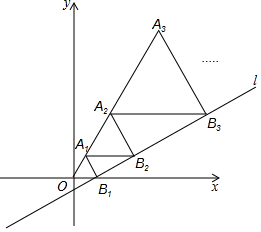 如图,在平面直角坐标系中,直线l:y=$\frac{\sqrt{3}}{3}$x-$\frac{\sqrt{3}}{3}$与x轴交于点B1,以OB1为边长作等边三角形A1OB1,过点A1作A1B2平行于x轴,交直线l于点B2,以A1B2为边长作等边三角形A2A1B2,过点A2作A2B3平行于x轴,交直线l于点B3,以A2B3为边长作等边三角形A3A2B3,…,则点A2017的横坐标是$\frac{{2}^{2017}-1}{2}$.
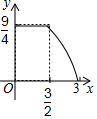
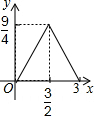
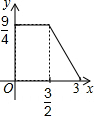
如图,在平面直角坐标系中,直线l:y=$\frac{\sqrt{3}}{3}$x-$\frac{\sqrt{3}}{3}$与x轴交于点B1,以OB1为边长作等边三角形A1OB1,过点A1作A1B2平行于x轴,交直线l于点B2,以A1B2为边长作等边三角形A2A1B2,过点A2作A2B3平行于x轴,交直线l于点B3,以A2B3为边长作等边三角形A3A2B3,…,则点A2017的横坐标是$\frac{{2}^{2017}-1}{2}$.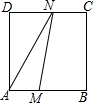 如图,在正方形ABCD中,AB=3cm,动点M自A点出发沿AB方向以每秒1cm的速度运动,同时动点N自D点出发沿折线DC-CB以每秒2cm的速度运动,到达B点时运动同时停止,设△AMN的面积为y(cm2),运动时间为x(秒),则下列图象中能大致反映y与x之间函数关系的是( )
如图,在正方形ABCD中,AB=3cm,动点M自A点出发沿AB方向以每秒1cm的速度运动,同时动点N自D点出发沿折线DC-CB以每秒2cm的速度运动,到达B点时运动同时停止,设△AMN的面积为y(cm2),运动时间为x(秒),则下列图象中能大致反映y与x之间函数关系的是( )