题目内容
5.化简:$\frac{x}{x-y}$-$\frac{y}{x+y}$,结果正确的是( )| A. | 1 | B. | $\frac{{x}^{2}+{y}^{2}}{{x}^{2}-{y}^{2}}$ | C. | $\frac{x-y}{x+y}$ | D. | x2+y2 |
分析 原式通分并利用同分母分式的减法法则计算即可得到结果.
解答 解:原式=$\frac{{x}^{2}+xy-xy+{y}^{2}}{{x}^{2}-{y}^{2}}$=$\frac{{x}^{2}+{y}^{2}}{{x}^{2}-{y}^{2}}$.
故选B
点评 此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
16.下列运算正确的是( )
| A. | (π-3)0=1 | B. | $\sqrt{9}$=±3 | C. | 2-1=-2 | D. | (-a2)3=a6 |
13.不等式组$\left\{\begin{array}{l}x-1≤0\\ 2x-5<1\end{array}\right.$的解集为( )
| A. | x<-2 | B. | x≤-1 | C. | x≤1 | D. | x<3 |
17.关于x的不等式组$\left\{\begin{array}{l}x-m<0\\ 3x-1>2({x-1})\end{array}\right.$无解,那么m的取值范围为( )
| A. | m≤-1 | B. | m<-1 | C. | -1<m≤0 | D. | -1≤m<0 |
9.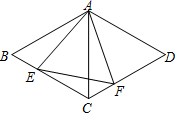 如图,菱形ABCD中,∠D=60°.点E、F分别在边BC、CD上,且BE=CF.若EF=2,则△AEF的面积为( )
如图,菱形ABCD中,∠D=60°.点E、F分别在边BC、CD上,且BE=CF.若EF=2,则△AEF的面积为( )
 如图,菱形ABCD中,∠D=60°.点E、F分别在边BC、CD上,且BE=CF.若EF=2,则△AEF的面积为( )
如图,菱形ABCD中,∠D=60°.点E、F分别在边BC、CD上,且BE=CF.若EF=2,则△AEF的面积为( )| A. | $4\sqrt{3}$ | B. | $3\sqrt{3}$ | C. | $2\sqrt{3}$ | D. | $\sqrt{3}$ |
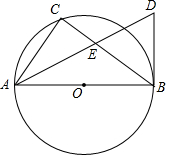 如图,AB是⊙O直径,点C在⊙O上,AD平分∠CAB,BD是⊙O的切线,AD与BC相交于点E.
如图,AB是⊙O直径,点C在⊙O上,AD平分∠CAB,BD是⊙O的切线,AD与BC相交于点E.