题目内容
4.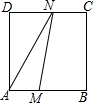 如图,在正方形ABCD中,AB=3cm,动点M自A点出发沿AB方向以每秒1cm的速度运动,同时动点N自D点出发沿折线DC-CB以每秒2cm的速度运动,到达B点时运动同时停止,设△AMN的面积为y(cm2),运动时间为x(秒),则下列图象中能大致反映y与x之间函数关系的是( )
如图,在正方形ABCD中,AB=3cm,动点M自A点出发沿AB方向以每秒1cm的速度运动,同时动点N自D点出发沿折线DC-CB以每秒2cm的速度运动,到达B点时运动同时停止,设△AMN的面积为y(cm2),运动时间为x(秒),则下列图象中能大致反映y与x之间函数关系的是( )| A. | 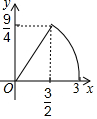 | B. |  | C. |  | D. | 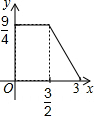 |
分析 分两部分计算y的关系式:①当点N在CD上时,易得S△AMN的关系式,S△AMN的面积关系式为一个一次函数;②当点N在CB上时,底边AM不变,表示出S△AMN的关系式,S△AMN的面积关系式为一个开口向下的二次函数.
解答  解:∵点N自D点出发沿折线DC-CB以每秒2cm的速度运动,到达B点时运动同时停止,
解:∵点N自D点出发沿折线DC-CB以每秒2cm的速度运动,到达B点时运动同时停止,
∴N到C的时间为:t=3÷2=1.5,
分两部分:
①当0≤x≤1.5时,如图1,此时N在DC上,
S△AMN=y=$\frac{1}{2}$AM•AD=$\frac{1}{2}$x×3=$\frac{3}{2}$x,
②当1.5<x≤3时,如图2,此时N在BC上,
∴DC+CN=2x,
∴BN=6-2x,
∴S△AMN=y=$\frac{1}{2}$AM•BN=$\frac{1}{2}$x(6-2x)=-x2+3x,
故选A.
点评 本题考查动点问题的函数图象问题;根据自变量不同的取值范围得到相应的函数关系式是解决本题的关键.

练习册系列答案
相关题目
16.下列运算正确的是( )
| A. | (π-3)0=1 | B. | $\sqrt{9}$=±3 | C. | 2-1=-2 | D. | (-a2)3=a6 |
13.不等式组$\left\{\begin{array}{l}x-1≤0\\ 2x-5<1\end{array}\right.$的解集为( )
| A. | x<-2 | B. | x≤-1 | C. | x≤1 | D. | x<3 |
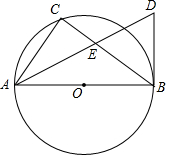 如图,AB是⊙O直径,点C在⊙O上,AD平分∠CAB,BD是⊙O的切线,AD与BC相交于点E.
如图,AB是⊙O直径,点C在⊙O上,AD平分∠CAB,BD是⊙O的切线,AD与BC相交于点E.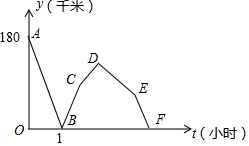 一辆轿车从甲城驶往乙城,同时一辆卡车从乙城驶往甲城,两车沿相同路线匀速行驶,轿车到达乙城停留一段时间后,按原路原速返回甲城;卡车到达甲城比轿车返回甲城早0.5小时,轿车比卡车每小时多行驶60千米,两车到达甲城后均停止行驶,两车之间的路程y(千米)与轿车行驶时间t(小时)的函数图象如图所示,请结合图象提供的信息解答下列问题:
一辆轿车从甲城驶往乙城,同时一辆卡车从乙城驶往甲城,两车沿相同路线匀速行驶,轿车到达乙城停留一段时间后,按原路原速返回甲城;卡车到达甲城比轿车返回甲城早0.5小时,轿车比卡车每小时多行驶60千米,两车到达甲城后均停止行驶,两车之间的路程y(千米)与轿车行驶时间t(小时)的函数图象如图所示,请结合图象提供的信息解答下列问题: 如图,四边形ABCD内接于⊙O,点E在BC的延长线上,若∠BOD=120°,则∠DCE=60°.
如图,四边形ABCD内接于⊙O,点E在BC的延长线上,若∠BOD=120°,则∠DCE=60°.