题目内容
5.在△ABC中,AB=BC,∠B=90°,将△ABC沿BC方向平移,得到△A'CC',以C为位似中心,作△DEC与△ABC位似,位似比为1:2,若F为CC'的中点,连接DF,A'F,则$\frac{A'F}{DF}$的值为1或$\sqrt{5}$.分析 设AB=BC=2x,①如图1,当点D在AC上时,根据平移的性质及中点的定义得出CF=x,继而可得A′F=$\sqrt{A′{C}^{2}+C{F}^{2}}$=$\sqrt{5}$x,由位似图形的性质可得DE=CE=x、EF=2x,继而知DF=$\sqrt{D{E}^{2}+E{F}^{2}}$=$\sqrt{5}$x,即可得$\frac{A'F}{DF}$的值;②如图2,当点D在AC延长线上时,由①知A′F=$\sqrt{A′{C}^{2}+C{F}^{2}}$=$\sqrt{5}$x,DF=DE=x,即可得$\frac{A'F}{DF}$的值.
解答 解:设AB=BC=2x,
①如图1,当点D在AC上时,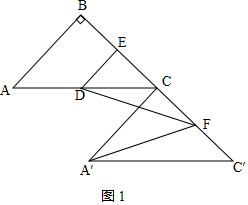
∵△ABC≌△A′CC′,
∴A′C=CC′=2x,
∵F为CC'的中点,
∴CF=x,
则A′F=$\sqrt{A′{C}^{2}+C{F}^{2}}$=$\sqrt{5}$x,
又∵△DEC∽△ABC,且$\frac{DE}{AB}$=$\frac{CE}{CB}$=$\frac{1}{2}$,
∴DE=CE=x,
则EF=2x,
∴DF=$\sqrt{D{E}^{2}+E{F}^{2}}$=$\sqrt{5}$x,
∴$\frac{A'F}{DF}$=$\frac{\sqrt{5}x}{\sqrt{5}x}$=1;
②如图2,当点D在AC延长线上时,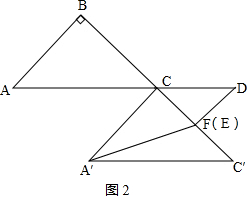
由①知A′F=$\sqrt{A′{C}^{2}+C{F}^{2}}$=$\sqrt{5}$x,DF=DE=x,
∴$\frac{A'F}{DF}$=$\frac{\sqrt{5}x}{x}$=$\sqrt{5}$,
故答案为:1或$\sqrt{5}$.
点评 本题主要考查平移的性质及位似图形的性质、勾股定理,熟练掌握平移的性质及位似图形的性质是解题的关键.

| A. | -2 | B. | ±2 | C. | 2 | D. | $\sqrt{2}$ |
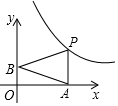 如图,已知动点A,B分别在x轴,y轴正半轴上,动点P在反比例函数y=$\frac{6}{x}$(x>0)图象上,PA⊥x轴,△PAB是以PA为底边的等腰三角形.当点A的横坐标逐渐增大时,△PAB的面积将会( )
如图,已知动点A,B分别在x轴,y轴正半轴上,动点P在反比例函数y=$\frac{6}{x}$(x>0)图象上,PA⊥x轴,△PAB是以PA为底边的等腰三角形.当点A的横坐标逐渐增大时,△PAB的面积将会( )| A. | 越来越小 | B. | 越来越大 | C. | 不变 | D. | 先变大后变小 |
| A. | 8 | B. | 10 | C. | 8或10 | D. | 以上都不正确 |
 如图,AB为⊙O的切线,切点为B,连接AO,AO与⊙O交于点C,BD为⊙O的直径,连接CD,若∠A=30°,⊙O的半径为2,则图中阴影部分的面积为$\frac{4}{3}$π-$\sqrt{3}$(结果保留π)
如图,AB为⊙O的切线,切点为B,连接AO,AO与⊙O交于点C,BD为⊙O的直径,连接CD,若∠A=30°,⊙O的半径为2,则图中阴影部分的面积为$\frac{4}{3}$π-$\sqrt{3}$(结果保留π)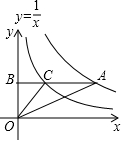 如图,在直角坐标系中,Rt△OAB的边在y轴上,∠ABO=90°,∠BOC=∠A=30°,双曲线y=$\frac{1}{x}$经过点C,双曲线y=$\frac{k}{x}$经过点A,则k的值为3.
如图,在直角坐标系中,Rt△OAB的边在y轴上,∠ABO=90°,∠BOC=∠A=30°,双曲线y=$\frac{1}{x}$经过点C,双曲线y=$\frac{k}{x}$经过点A,则k的值为3.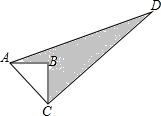 如图,△ABC中,∠B=90°,AB=3,BC=4,若CD=12,AD=13.求阴影部分的面积.
如图,△ABC中,∠B=90°,AB=3,BC=4,若CD=12,AD=13.求阴影部分的面积.