题目内容
10.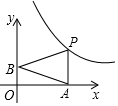 如图,已知动点A,B分别在x轴,y轴正半轴上,动点P在反比例函数y=$\frac{6}{x}$(x>0)图象上,PA⊥x轴,△PAB是以PA为底边的等腰三角形.当点A的横坐标逐渐增大时,△PAB的面积将会( )
如图,已知动点A,B分别在x轴,y轴正半轴上,动点P在反比例函数y=$\frac{6}{x}$(x>0)图象上,PA⊥x轴,△PAB是以PA为底边的等腰三角形.当点A的横坐标逐渐增大时,△PAB的面积将会( )| A. | 越来越小 | B. | 越来越大 | C. | 不变 | D. | 先变大后变小 |
分析 设点P(x,$\frac{6}{x}$),作BC⊥PA可得BC=OA=x,根据S△PAB=$\frac{1}{2}$PA•BC=$\frac{1}{2}$•$\frac{6}{x}$•x=3可得答案.
解答 解:如图,过点B作BC⊥PA于点C,
则BC=OA,
设点P(x,$\frac{6}{x}$),
则S△PAB=$\frac{1}{2}$PA•BC=$\frac{1}{2}$•$\frac{6}{x}$•x=3,
当点A的横坐标逐渐增大时,△PAB的面积将会不变,始终等于3,
故选:C.
点评 本题主要考查反比例函数系数k的几何意义,熟练掌握在反比例函数的图象上任意一点向坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是$\frac{1}{2}$|k|,且保持不变.

练习册系列答案
相关题目
20.下列结论正确的是( )
| A. | 形状相同的两个图形是全等图形 | B. | 全等图形的面积相等 | ||
| C. | 对应角相等的两个三角形全等 | D. | 两个等边三角形全等 |
1.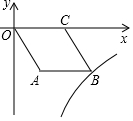 如图,O是坐标原点,菱形OABC的顶点A的坐标为(6,-8),顶点C在x轴的正半轴上,若函数y=$\frac{k}{x}$(x>0)的图象经过顶点B,则k的值为( )
如图,O是坐标原点,菱形OABC的顶点A的坐标为(6,-8),顶点C在x轴的正半轴上,若函数y=$\frac{k}{x}$(x>0)的图象经过顶点B,则k的值为( )
 如图,O是坐标原点,菱形OABC的顶点A的坐标为(6,-8),顶点C在x轴的正半轴上,若函数y=$\frac{k}{x}$(x>0)的图象经过顶点B,则k的值为( )
如图,O是坐标原点,菱形OABC的顶点A的坐标为(6,-8),顶点C在x轴的正半轴上,若函数y=$\frac{k}{x}$(x>0)的图象经过顶点B,则k的值为( )| A. | -48 | B. | -64 | C. | -96 | D. | -128 |
15.某品牌商品,按标价八折出售,仍可获得20%的利润,若该商品标价为18元,则该商品的进价为( )
| A. | 13元 | B. | 12元 | C. | 15元 | D. | 16元 |
19.如果不等式组$\left\{\begin{array}{l}{-1<x≤3}\\{x>m}\end{array}\right.$ 有解,那么m的取值范围是( )
| A. | m≤3 | B. | m<3 | C. | m<-1 | D. | -1<m<3 |